Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T17:57:58.661Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth Estimates on Positive Solutions of the Equation

Published online by Cambridge University Press:  20 November 2018

Man Chun Leung
Man Chun Leung*
Affiliation:
Department of Mathematics National University of Singapore 2 Science Drive 2 Singapore 117543 Republic of Singapore, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct unbounded positive 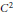${{C}^{2}}$-solutions of the equation 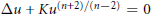$\Delta u\,+\,K{{u}^{\left( n+2 \right)/\left( n-2 \right)}}\,=\,0$ in 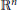${{\mathbb{R}}^{n}}$ (equipped with Euclidean metric 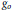${{g}_{0}}$) such that 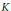$K$ is bounded between two positive numbers in 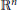${{\mathbb{R}}^{n}}$, the conformal metric 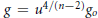$g\,=\,{{u}^{4/\left( n-2 \right)}}{{g}_{0}}$ is complete, and the volume growth of 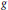$g$ can be arbitrarily fast or reasonably slow according to the constructions. By imposing natural conditions on 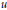$u$, we obtain growth estimate on the 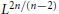${{L}^{2n/\left( n-2 \right)}}$-norm of the solution and show that it has slow decay.

Keywords

35J6058G03positive solutionconformal scalar curvature equationgrowth estimate
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 2 , 01 June 2001 , pp. 210 - 222
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Caffarelli, L., Gidas, B. and Spruck, J., Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth. Comm. Pure Appl. Math. 42 (1989), 271–297.Google Scholar
[2] Chen, C.-C. and Lin, C.-S., On compactness and completeness of conformal metrics in R N . Asian J. Math. 1 (1997), 549–559.Google Scholar
[3] Chen, C.-C. and Lin, C.-S., Estimates of the conformal scalar curvature equation via the method of moving planes. Comm. Pure Appl. Math. 50 (1997), 971–1019.Google Scholar
[4] Chen, C.-C. and Lin, C.-S., Estimates of the conformal scalar curvature equation via the method of moving planes. II. J. Differential Geom. 49 (1998), 115–178.Google Scholar
[5] Chen, C.-C. and Lin, C.-S., On the asymptotic symmetry of singular solutions of the scalar curvature equations. Math. Ann. 313 (1999), 229–245.Google Scholar
[6] Cheung, K.-L. and Leung, M.-C., Asymptotic behavior of positive solutions of the equation and positive scalar curvature. Preprint.Google Scholar
[7] Ding, W.-Y. and Ni, W.-M., On the elliptic equation and related topics. Duke Math. J. 52 (1985), 485–506.Google Scholar
[8] Korevaar, N., Mazzeo, R., Pacard, F. and Schoen, R., Refined asymptotics for constant scalar curvature metrics with isolated singularities. Invent.Math. 135 (1999), 233–272.Google Scholar
[9] Gromov, M., Positive curvature, macroscopic dimension, spectral gaps, and higher signatures. Functional Analysis on the Eve of the 21st Century, Volume II, pp. 1–213, Progress in Mathematics 132, Birkhäuser, Boston, 1995.Google Scholar
[10] Leung, M.-C., Conformal scalar curvature equations on complete manifolds. Comm. Partial Differential Equations 20 (1995), 367–417.Google Scholar
[11] Leung, M.-C., Asymptotic behavior of positive solutions of the equation in a complete Riemannian manifold and positive scalar curvature. Comm. Partial Differential Equations 24 (1999), 425–462.Google Scholar
[12] Lin, C.-S., Estimates of the conformal scalar curvature equation via the method of moving planes. III. Comm. Pure Appl. Math. 53 (2000), 611–646.Google Scholar
[13] Taliaferro, S., On the growth of superharmonic functions near an isolated singularity, I. J. Differential Equations 158 (1999), 28–47.Google Scholar