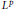Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T01:34:45.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Cohomology and ${{L}^{p}}$-Cohomology of Finitely Generated Groups

Published online by Cambridge University Press:  20 November 2018

Michael J. Puls
Michael J. Puls*
Affiliation:
Department of Mathematics, Eastern Oregon University, One University Boulevard, La Grande, OR 97850, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $G$ be a finitely generated, infinite group, let 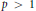$p\,>\,1$, and let 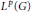${{L}^{p}}\left( G \right)$ denote the Banach space 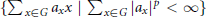$\left\{ \sum{_{x\in G}{{a}_{x}}x}|\sum{_{x\in G}|{{a}_{x}}{{|}^{p}}<\infty } \right\}$. In this paper we will study the first cohomology group of $G$ with coefficients in 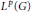${{L}^{p}}\left( G \right)$, and the first reduced 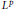${{L}^{p}}$-cohomology space of $G$. Most of our results will be for a class of groups that contains all finitely generated, infinite nilpotent groups.

Keywords

43A1520F6520F18group cohomologyLp-cohomologycentral element of infinite orderharmonic functioncontinuous linear functional
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 268 - 276
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Houghton, C. H., Ends of groups and the associated first cohomology groups. J. LondonMath. Soc. (2) 6 (1972), 81–92.Google Scholar
[2] Maeda, Fumi-Yuki, A remark on parabolic index of infinite networks. Hiroshima Math. J. (1) 7 (1977), 147–152.Google Scholar
[3] Wayne Roberts, A. and Varberg, Dale E., Convex functions. Academic Press, A subsidiary of Harcourt Brace Jovanovich, Pure and Appl. Math., New York, London, 1973.Google Scholar
[4] Soardi, Paolo M. and Woess, Wolfgang, Uniqueness of currents in infinite resistive networks. Discrete Appl. Math. (1) 31 (1991), 37–49.Google Scholar
[5] Varopoulos, N. Th., Isoperimetric inequalities and Markov chains. J. Funct. Anal. (2) 63 (1985), 215–239.Google Scholar