Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-08T15:27:03.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Actions, Cyclic Coverings and Families of K3-Surfaces

Published online by Cambridge University Press:  20 November 2018

Alessandra Sarti
Alessandra Sarti*
Affiliation:
Fachbereich für Mathematik, Johannes Gutenberg-Universität, 55099 Mainz, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we describe six pencils of 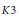$K3$-surfaces which have large Picard number 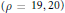$\left( \rho =19,20 \right)$ and each contains precisely five special fibers: four have 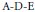$\text{A-D-E}$ singularities and one is non-reduced. In particular, we characterize these surfaces as cyclic coverings of some 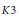$K3$-surfaces described in a recent paper by Barth and the author. In many cases, using 3-divisible sets, resp., 2-divisible sets, of rational curves and lattice theory, we describe explicitly the Picard lattices.

Keywords

14J2814L3014E2014C22
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 4 , 01 December 2006 , pp. 592 - 608
Copyright
Copyright © Canadian Mathematical Society 2006

References

[BPV] Barth, W., Peters, C., and Van de Ven, A., Compact Complex Surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 3, Band 4, Springer-Verlag, Berlin, 1984.Google Scholar
[BS] Barth, W. and Sarti, A., Polyhedral groups and pencils of K3-surfaces with maximal Picard number. Asian J. Math. 7(2003), no. 4, 519–538.Google Scholar
[Be] Belcastro, S.-M., Picard lattices of families of K3 surfaces. Comm. Alg. 30(2002), no. 1, 61–82.Google Scholar
[D] Dolgachev, I. V., Mirror symmetry for lattice polarized K3 surfaces. J. Math. Sci. 81(1996), no. 3, 2599–2630.Google Scholar
[I] Inose, H., On certain Kummer surfaces which can be realized as non-singular quartic surfaces in ℙ 3 . J. Fac. Sci. Univ. Tokyo Sect. IA Math. 23(1976), no. 3, 545–560.Google Scholar
[M1] Miranda, R., Triple covers in algebraic geometry.. Amer. J. Math. 107(1985), no. 5, 1123–1158.Google Scholar
[M2] Miranda, R., Algebraic Curves and Riemann Surfaces. Graduate Studies in Mathematics 5, American Mathematical Society, Providence, RI, 1995.Google Scholar
[Mo] Morrison, D. R., On K3 surfaces with large Picard number. Invent.Math. 75(1984), no. 1, 105–121.Google Scholar
[N] Nikulin, V. V., On Kummer Surfaces. Izv. Akad. Nauk SSSR Ser. Math. 39(1975), no. 2, 278–293, 471.Google Scholar
[S1] Sarti, A., Pencils of symmetric surfaces in ℙ 3 . J. Algebra 246(2001), no. 1, 429–452.Google Scholar
[S2] Sarti, A., Symmetric surfaces with many singularities. Comm. Algebra 32(2004), no. 10, 3745–3770.Google Scholar
[SI] Shioda, T. and Inose, H., On singular K3 surfaces. In: Complex Analysis and Algebraic Geometry. Iwanami Shoten, Tokyo, 1977, pp. 119–136..Google Scholar
[T] Tan, S. L., Cusps on some algebraic surfaces and plane curves, preprint.Google Scholar
[vGT] van Geemen, B. and Top, J., An isogeny of K3 surfaces, to appear in Bull. London Math. Soc.Google Scholar
[VY] Verril, H. and Yui, N., Thompson series and the mirror maps of pencils of K3 surfaces. In: The Arithmetic and Geometry of Algebraic Cycles. CRM Proc. Lecture Notes 24, Amer. Math. Soc. Providence, RI, 2000, pp. 399–432.Google Scholar