Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ne?et?il, Jaroslav
1972.
On symmetric and antisymmetric relations.
Monatshefte f�r Mathematik,
Vol. 76,
Issue. 4,
p.
323.
Hell, P.
1972.
Full embeddings into some categories of graphs.
Algebra Universalis,
Vol. 2,
Issue. 1,
p.
129.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
Hell, Pavol
1974.
On some strongly rigid families of graphs and the full embeddings they induce.
Algebra Universalis,
Vol. 4,
Issue. 1,
p.
108.
Fried, E.
and
Wiegandt, R.
1975.
Connectednesses and disconnectednesses of graphs.
Algebra Universalis,
Vol. 5,
Issue. 1,
p.
411.
Kučera, Luděk
1975.
On universal concrete categories.
Algebra Universalis,
Vol. 5,
Issue. 1,
p.
149.
Babai, L.
1977.
Asymmetric trees with two prescribed degrees.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 29,
Issue. 1-2,
p.
193.
Nešetřil, Jaroslav
and
Pultr, Aleš
1978.
On classes of relations and graphs determined by subobjects and factorobjects.
Discrete Mathematics,
Vol. 22,
Issue. 3,
p.
287.
Hell, P.
and
Ne?et?il, J.
1978.
Homomorphisms of graphs and of their orientations.
Monatshefte f�r Mathematik,
Vol. 85,
Issue. 1,
p.
39.
Nešetřil, J.
1979.
AMALGAMATION OF GRAPHS AND ITS APPLICATIONS.
Annals of the New York Academy of Sciences,
Vol. 319,
Issue. 1,
p.
415.
Hell, Pavol
and
Nešetřil, Jaroslav
1979.
Cohomomorphisms of graphs and hypergraphs.
Mathematische Nachrichten,
Vol. 87,
Issue. 1,
p.
53.
Hell, Pavol
1979.
AN INTRODUCTION TO THE CATEGORY OF GRAPHS*.
Annals of the New York Academy of Sciences,
Vol. 328,
Issue. 1,
p.
120.
1980.
Combinatorial, Algebraic and Topological Representations of Groups, Semigroups and Categories.
Vol. 22,
Issue. ,
p.
353.
Babai, László
and
Pultr, Aleš
1980.
Endomorphism monoids and topological subgraphs of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 28,
Issue. 3,
p.
278.
D�rfler, W.
and
Waller, D. A.
1980.
A category-theoretical approach to hypergraphs.
Archiv der Mathematik,
Vol. 34,
Issue. 1,
p.
185.
Babai, László
and
Nešetřil, Jaroslav
1982.
Algebraic and Geometric Combinatorics.
Vol. 65,
Issue. ,
p.
55.
Koubek, Václav
and
Rödl, Vojtěch
1984.
On the minimum order of graphs with given semigroup.
Journal of Combinatorial Theory, Series B,
Vol. 36,
Issue. 2,
p.
135.
Zemlyachenko, V. N.
Korneenko, N. M.
and
Tyshkevich, R. I.
1985.
Graph isomorphism problem.
Journal of Soviet Mathematics,
Vol. 29,
Issue. 4,
p.
1426.
Koubek, V.
and
Sichler, J.
1985.
Quotients of rigid (0,1)-lattices.
Archiv der Mathematik,
Vol. 44,
Issue. 5,
p.
403.
Goralčík, Pavel
and
Koubek, Václav
1986.
Verifying nonrigidity.
Information Processing Letters,
Vol. 22,
Issue. 2,
p.
91.
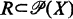 . This interpretation is generalized in the notion of society.
. This interpretation is generalized in the notion of society.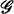 is a couple (X, R), where
is a couple (X, R), where 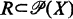 ; a k-society is a society (X, R) with |A| = k for each A ∊ R.
; a k-society is a society (X, R) with |A| = k for each A ∊ R.