Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T11:32:16.055Z Has data issue: false hasContentIssue false
  • English
  • Français

The Grade Conjecture and the S2 Condition

Published online by Cambridge University Press:  20 November 2018

Agustín Marcelo ,
Félix Marcelo  and
César Rodríguez
Agustín Marcelo
Affiliation:
Departamento de Matemáticas, Universidad de Las Palmas de Gran Canaria, Campus de Tafira, 35017 Las Palmas de Gran Canaria, Spain, email: [email protected]@[email protected]
Félix Marcelo
Affiliation:
Departamento de Matemáticas, Universidad de Las Palmas de Gran Canaria, Campus de Tafira, 35017 Las Palmas de Gran Canaria, Spain, email: [email protected]@[email protected]
César Rodríguez
Affiliation:
Departamento de Matemáticas, Universidad de Las Palmas de Gran Canaria, Campus de Tafira, 35017 Las Palmas de Gran Canaria, Spain, email: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Sufficient conditions are given in order to prove the lowest unknown case of the grade conjecture. The proof combines vanishing results of local cohomology and the 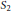${{S}_{2}}$ condition.

Keywords

13D2213D4513D2513C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 1 , 01 March 2002 , pp. 119 - 122
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Hartshorne, R., Algebraic Geometry. Springer, New York, 1977.Google Scholar
[2] Hochster, M., Topics in the homological theory of modules over commutative rings. CBMS Regional conference series 24, Amer.Math. Soc., 1975.Google Scholar
[3] Matsumura, H., Commutative Algebra. Benjamin, 1970.Google Scholar
[4] Peskine, C. and Szpiro, L., Syzygies et Multiplicités. C. R. Acad. Sci. Paris, Sér. A 278 (1974), 1421–1424.Google Scholar
[5] Roberts, P., The Homological Conjectures. In: Free Resolutions in Commutative Algebra and Algebraic Geometry, (eds. D. Eisenbud, C. Huneke), Res. Notes Math. 2, D. Jones and Bartlett Publishers, Boston, 1992, 121–132.Google Scholar