Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T06:48:50.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Going-Down Results for Ci-Fields

Published online by Cambridge University Press:  20 November 2018

Anthony J. Bevelacqua  and
Mark J. Motley
Anthony J. Bevelacqua
Affiliation:
Department of Mathematics, University of North Dakota, Grand Forks, North Dakota 58202, USA email: [email protected]
Mark J. Motley
Affiliation:
Department of Mathematics, Pikeville College, Pikeville, Kentucky 41501, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We search for theorems that, given a 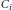${{C}_{i}}$-field 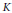$K$ and a subfield 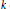$k$ of 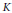$K$, allow us to conclude that 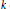$k$ is a 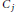${{C}_{j}}$ -field for some 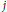$j$. We give appropriate theorems in the case 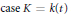$\text{case }K=k\left( t \right)$ and 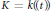$K=k\left( \left( t \right) \right)$. We then consider the more difficult case where 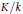$K/k$ is an algebraic extension. Here we are able to prove some results, and make conjectures. We also point out the connection between these questions and Lang's conjecture on nonreal function fields over a real closed field.

Keywords

12F14GCi-fieldsLang's Conjecture
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 1 , 01 March 2006 , pp. 11 - 20
Copyright
Copyright © Canadian Mathematical Society 2006

References

[Be-Ma] Becker, M. F. and MacLane, S., The Minimum Number of Generators for Inseparable Algebraic Extensions. Bull. Amer. Math. Soc. 46(1940), 182–186.Google Scholar
[Be-Mo] Bevelacqua, A. and Motley, M., Finite Codimension Subfields of a Field Complete with Respect to a Real Valuation. Comm. Algebra, to appear.Google Scholar
[C] Cohen, I. S., On the Structure and Ideal Theory of Complete Local Rings. Trans. Amer. Math. Soc. (1) 59(1946), 54–106.Google Scholar
[G] Greenberg, Marvin J., Lectures on Forms in Many Variables. Benjamin, 1969.Google Scholar
[J] Jacobson, Nathan, Lectures in Abstract Algebra Volume 3. Van Nostrand, San Francisco, 1964.Google Scholar
[L] Lang, S., On Quasi-Algebraic Closure. Ann. of Math. 55(1952), 373–390.Google Scholar
[N] Neukirch, Jurgen, Algebraic Number Theory. Grundlehren der Mathematischen Wissenschaften 322, Springer, 1999.Google Scholar
[P] Pfister, Albrecht, Quadratic Forms with Applications to Algebraic Geometry and Topology. Cambridge University Press, 1995.Google Scholar
[S] Serre, J. P., Local Fields. Springer-Verlag, New York, 1979.Google Scholar
[Te] Teichmuller, O., p-Algebren. Deutsche Math. 1(1936), 362–388.Google Scholar
[Ts] Tsen, C., Zur Stufentheorie der Quasi-algebraisch-Abgeschlossenheit kommutativer Körper. J. Chinese Math. Soc. 171(1936), 81–92.Google Scholar
[Z-S] Zariski, Oscar and Samuel, Pierre, Commutative Algebra Volume 2. Springer-Verlag, 1960.Google Scholar