Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T10:05:56.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Globalization of Distinguished Supercuspidal Representations of GL(n)

Published online by Cambridge University Press:  20 November 2018

Jeffrey Hakim  and
Fiona Murnaghan
Jeffrey Hakim
Affiliation:
Department of Mathematics and Statistics, American University, 4400 Massachusetts Avenue NW, Washington, DC 20016, U.S.A., e-mail: [email protected]
Fiona Murnaghan
Affiliation:
Department of Mathematics, University of Toronto, 100 Saint George Street, Toronto, Ontario, M5S 3G3, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An irreducible supercuspidal representation 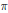$\pi$ of 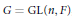$G\,=\,\text{GL}\left( n,\,F \right)$, where $F$ is a nonarchimedean local field of characteristic zero, is said to be “distinguished” by a subgroup 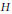$H$ of 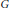$G$ and a quasicharacter 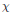$\text{ }\!\!\chi\!\!\text{ }$ of 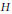$H$ if 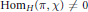$\text{Ho}{{\text{m}}_{H}}\left( \pi ,\,\text{ }\!\!\chi\!\!\text{ } \right)\,\ne \,0$. There is a suitable global analogue of this notion for an irreducible, automorphic, cuspidal representation associated to 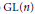$\text{GL}\left( n \right)$. Under certain general hypotheses, it is shown in this paper that every distinguished, irreducible, supercuspidal representation may be realized as a local component of a distinguished, irreducible automorphic, cuspidal representation. Applications to the theory of distinguished supercuspidal representations are provided.

Keywords

22E5022E3511F70
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 2 , 01 June 2002 , pp. 220 - 230
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bernstein, J., Deligne, P. and Kazhdan, D., Trace Paley-Weiner theorem for reductive p-adic groups. J. Anal.Math. 47 (1986), 47–1986.Google Scholar
[2] Bernstein, J., Deligne, P., Kazhdan, D. and Vignéras, M.-F., Representations des groupes sur un corps local. Hermann, Paris, 1984.Google Scholar
[3] Clozel, L., Invariant harmonic analysis on the Schwartz space of a reductive p-adic group. In: Harmonic Analysis on Reductive Groups, (eds.W. Barker and P. Sally), Progress in Math. 101, Birkäuser, Boston, 1991, 101–121.Google Scholar
[4] Flicker, Y., On distinguished representations. J. Reine Angew. Math. 418 (1991), 418–1991.Google Scholar
[5] Friedberg, S. and Jacquet, H., Linear periods. J. Reine Angew. Math. 443 (1993), 443–1993.Google Scholar
[6] Gelbart, S., Lectures on the Arthur-Selberg Trace Formula. University Lecture Series 9, Amer. Math. Soc., Providence, RI, 1996.Google Scholar
[7] Gelfand, I. and Kazhdan, D., Representations of GL(n, K) where K is a local field. Lie Groups and Their Representations, Wiley, New York, 1975, 95–118.Google Scholar
[8] Hakim, J., Admissible distributions on p-adic symmetric spaces. J. Reine Angew. Math. 455 (1994), 455–1994.Google Scholar
[9] Hakim, J., Distinguished p-adic representations. Duke Math. J. (1) 62 (1991), 62–1991.Google Scholar
[10] Hakim, J. and Mao, Z., Cuspidal representations associated to (GL(n), O(n)) over finite fields and p-adic fields. J. Algebra 213 (1999), 213–1999.Google Scholar
[11] Hakim, J. and Mao, Z., Supercuspidal representations of GL(n) distinguished by a unitary subgroup. Pacific J. Math. 185 (1998), 185–1998.Google Scholar
[12] Hakim, J. and Murnaghan, F., Tame supercuspidal representations of GL(n) distinguished by a unitary subgroup. preprint.Google Scholar
[13] Harder, G., Langlands, R. and Rapoport, M., Algebraische Zyklen auf Hilbert-Blumenthal-Flächen. J. Reine Angew. Math. 366 (1986), 366–1986.Google Scholar
[14] Heumos, M. and Rallis, S., Symplectic-Whittaker models for GLn . Pacific J. Math. 146 (1990), 146–1990.Google Scholar
[15] Jacquet, H. and Rallis, S., Symplectic periods. J. Reine Angew. Math. 423 (1992), 423–1992.Google Scholar
[16] Jacquet, H. and Rallis, S., Uniqueness of linear periods. Comp. Math. 102 (1996), 102–1996.Google Scholar
[17] Jacquet, H. and Ye, Y., Distinguished representations and quadratic base change for GL(3). Trans. Amer. Math. Soc. Paris (3) 348 (1996), 348–1996.Google Scholar
[18] Jacquet, H. and Ye, Y., Une remarque sur le changement de base quadratique. C. R. Acad. Sci. Paris Sér I 311 (1990), 311–1990.Google Scholar
[19] Prasad, D., On the self-dual representations of a p-adic group. preprint.Google Scholar