Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:28:29.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Global Hypoellipticity of a Class of Second Order Operators

Published online by Cambridge University Press:  20 November 2018

Adalberto P. Bergamasco  and
Sérgio Luís Zani
Adalberto P. Bergamasco
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, Caixa Postal 676-13.565-905, São Carlos, SP Brazil e-mail:, [email protected]
Sérgio Luís Zani
Affiliation:
Instituto de Ciências Matemdticas de São Carlos, Universidade de São Paulo, Caixa Postal 668-13.560-970, São Carlos, SP Brazil
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that almost all perturbations P — λ, λ € C, of an arbitrary constant coefficient partial differential operator P are globally hypoelliptic on the torus. We also give a characterization of the values λ € C for which the operator 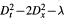is globally hypoelliptic; in particular, we show that the addition of a term of order zero may destroy the property of global hypoellipticity of operators of principal type, contrary to that happens with the usual (local) hypoellipticity.

Keywords

35H0535B1035B65global hypoellipticityperiodic solutions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 3 , 01 September 1994 , pp. 301 - 305
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Greenfield, S.J., and Wallach, N., Global hypoellipticity and Liouville numbers, Proc. Amer. Math. Soc 31(1972), 112–114.Google Scholar
2. Greenfield, S.J., Remarks on global hypoellipticity, Trans. Amer. Math. Soc 183(1973), 153–164.Google Scholar
3. Herz, C. S., Functions which are divergences, Amer. J. Math. 92(1970), 641–656.Google Scholar
4. Leveque, W. J., Fundamentals of number theory, Reading, Addison-Wesley, 1977.Google Scholar
5. Mordell, L. J., Diophantine equations, New York, Academic Press, 1969.Google Scholar
6. Salamon, D. and Zehnder, E., KAM theory in configuration space, Comment. Math. Helv. 64(1989), 84–132.Google Scholar
7. Schwartz, L., Méthodes mathématiques pour les sciences physiques, Paris, Hermann, 1965.Google Scholar
8. Treves, F., Hypoelliptic partial differential equations of principal type. Sufficient conditions and necessary conditions. Comm. Pure Appl. Math. 34(1971), 631–670.Google Scholar
9. Yoshino, M., A class of globally hypoelliptic operators on the torus, Math. Z. 201(1989), 1–11.Google Scholar