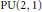Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cunha, Heleno
and
Gusevskii, Nikolay
2010.
On the moduli space of quadruples of points in the boundary of complex hyperbolic space.
Transformation Groups,
Vol. 15,
Issue. 2,
p.
261.
Xiao, Yingqing
and
Jiang, Yueping
2011.
Complex lines in complex hyperbolic space H ℂ 2.
Indian Journal of Pure and Applied Mathematics,
Vol. 42,
Issue. 5,
p.
279.
Cao, Wensheng
2016.
Congruence classes of points in quaternionic hyperbolic space.
Geometriae Dedicata,
Vol. 180,
Issue. 1,
p.
203.
Platis, Ioannis D.
2016.
Paired $$\mathrm{CR}$$ CR structures and the example of Falbel’s cross-ratio variety.
Geometriae Dedicata,
Vol. 181,
Issue. 1,
p.
257.
Platis, Ioannis D.
and
Sun, Li-Jie
2021.
A Kähler structure for the $$\text {PU}(2, 1)$$ configuration space of four points in $$S^3$$.
Geometriae Dedicata,
Vol. 214,
Issue. 1,
p.
609.
Cao, Wensheng
2022.
The moduli space of points in quaternionic projective space.
Hiroshima Mathematical Journal,
Vol. 52,
Issue. 3,
Rochberg, Richard
2024.
Geometry of Five Point Sets in the Complex Ball.
Complex Analysis and Operator Theory,
Vol. 18,
Issue. 3,