Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-12T09:08:49.793Z Has data issue: false hasContentIssue false
  • English
  • Français

The Global Attractor of a Damped, Forced Hirota Equation in H1

Published online by Cambridge University Press:  20 November 2018

Boling Guo  and
Zhaohui Huo
Boling Guo
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, 100088, P.R. China e-mail: [email protected]
Zhaohui Huo
Affiliation:
Institute of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100080, P.R. China, andDepartment of Mathematics, City University of Hong Kong, Kowloon, Hong Kong, P.R. China e-mail: [email protected] Department of Mathematics, City University of Hong Kong, Kowloon, Hong Kong, P.R. China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The existence of the global attractor of a damped forced Hirota equation in the phase space 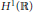${{H}^{1}}\left( \mathbb{R} \right)$ is proved. The main idea is to establish the so-called asymptotic compactness property of the solution operator by energy equation approach.

Keywords

35Q5335B4035B4137L30global attractorFourier restriction normdamping systemasymptotic compactness
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 295 - 310
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Abergel, F., Existence and finite dimensionality of the global attractor for evolution equations on unbounded domains. J. Differential Equations 83(1990), no. 1, 85–108. doi:10.1016/0022-0396(90)90070-6Google Scholar
[2] Bourgain, J., Fourier restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrödinger equation. Geom. Funct. Anal. 3(1993), no. 2, 107–156. doi:10.1007/BF01896020Google Scholar
[3] Bourgain, J., Fourier restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrödinger equation. II. The KdV equation. Geom. Funct. Anal. 3(1993), no. 3, 209–262. doi:10.1007/BF01895688Google Scholar
[4] Ghidaglia, J.-M., Weakly damped forced Korteweg-de Vries equations behave as a finite dimensional dynamical system in the long time. J. Differential Equations 74(1988), no. 2, 369–390. doi:10.1016/0022-0396(88)90010-1Google Scholar
[5] Ghidaglia, J.-M., A note on the strong convergence towards attractors of damped forced KdV equations. J. Differential Equations 110(1994), no. 2, 356–359. doi:10.1006/jdeq.1994.1071Google Scholar
[6] Goubet, O., Regularity of the global attractor for a weakly damped nonlinear Schrödinger equation in ℝ2 . Adv. Differential Equations 3(1998), no. 3, 337–360.Google Scholar
[7] Goubet, O., Asymptotic smoothing effect for weakly damped Korteweg-de Vries equations. Discrete Contin. Dynam. Systems, 6(2000), no. 3, 625–644.Google Scholar
[8] Goubet, O. and Rosa, R., Asymptotic smoothing and the global attractor of a weakly damped KdV equation on the real line. J. Differential Equations 185(2002), no. 1, 25–53. doi:10.1006/jdeq.2001.4163Google Scholar
[9] Guo, B. and Tan, S., Global smooth solution for nonlinear evolution equation of Hirota type. Sci. China, Ser. A 35(1992), no. 12, 1425–1433.Google Scholar
[10] Hasegawa, A., Optical Solitons in Fibers. Second edition. Springer, Berlin, 1990.Google Scholar
[11] Hasegawa, A. and Kodama, Y., Nonlinear pulse propagation in a monomode dielectric guide. IEEE J. Quantum Electronics. 23(1987), 510–524.Google Scholar
[12] Huo, Z. and Guo, B., Well-posedness of the Cauchy problem for the Hirota equation in Sobolev spaces Hs . Nonlinear Anal. 60(2005), no. 6, 1093–1110. doi:10.1016/j.na.2004.10.011Google Scholar
[13] Huo, Z. and Jia, Y., Well-posedness for the Cauchy problem to the Hirota equation in Sobolev spaces of negative indices. Chinese Ann. Math. Ser. B 26(2005), no. 1, 75–88. doi:10.1142/S0252959905000075Google Scholar
[14] Karachalios, N. and Stavrakakis, N., Global attractor for the weakly damped driven Schrödinger equation in H2R . NoDEA Nonlinear Differential Equations Appl. 9(2002), no. 3, 347–360. doi:10.1007/s00030-002-8132-yGoogle Scholar
[15] Kenig, C. E., Ponce, G., and Vega, L., The Cauchy problem for the Korteweg-de Vries equation in Sobolev spaces of negative indices. Duke Math. J. 71(1993), no. 1, 1–21. doi:10.1215/S0012-7094-93-07101-3Google Scholar
[16] Kenig, C. E., Ponce, G., and Vega, L., A bilinear estimate with applications to the Kdv equation. J. Amer. Math. Soc. 9(1996), no. 2, 573–603. doi:10.1090/S0894-0347-96-00200-7Google Scholar
[17] Kodama, Y., Optical solitons in a monomode fiber. J. Statist. Phys. 39(1985), no. 5–6, 597–614. doi:10.1007/BF01008354Google Scholar
[18] Ladyzhenskaya, O., Attractor for Semigroups and Evolution Equations. Lezioni Lincei, Cambridge University Press, 1991.Google Scholar
[19] Laurey, C., The Cauchy problem for a third order nonlinear Schrödinger equation. Nonlinear Anal. 29(1997), no. 2, 121–158. doi:10.1016/S0362-546X(96)00081-8Google Scholar
[20] Moise, I. and Rosa, R., On the regularity of the global attractor of a weakly damped, forced Korteweg-de Vries equation. Adv. Differential Equations 2(1997), no. 2, 275–296.Google Scholar
[21] Moise, I., Rosa, R., and Wang, X., Attractors for non-compact semigroups via energy equations. Nonlinearity 11(1998), no. 5, 1369–1393. doi:10.1088/0951-7715/11/5/012Google Scholar
[22] Rosa, R., The global attractor of a weakly damped, forced Korteweg-de Vries equation in H 1(ℝ) . Mat. Contemp. 19(2000), 129–152.Google Scholar
[23] Tan, S., Han, Y., Long time behavior of solutions to general nonlinear evolution equations. Chinese Ann. Math. Ser. A 16(1995), no. 2, 127–141.Google Scholar
[24] Temam, R., Infinite Dimensional Dynamical Systems in Mechanics and Physics. Second edition. Applied Mathematical Sciences 68, Springer-Verlag, New York, 1997.Google Scholar