Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T19:17:58.157Z Has data issue: false hasContentIssue false
  • English
  • Français

Ghosts and Strong Ghosts in the Stable Category

Published online by Cambridge University Press:  20 November 2018

Jon F. Carlson ,
Sunil K. Chebolu  and
Ján Mináč
Jon F. Carlson
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, USA e-mail: [email protected]
Sunil K. Chebolu
Affiliation:
Department of Mathematics, Illinois State University, Normal, IL 61790 USA e-mail: [email protected]
Ján Mináč
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7, Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 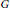$G$ is a finite group and $k$ is a field of characteristic 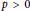$p\,>\,0$. A ghost map is a map in the stable category of finitely generated 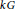$kG$-modules which induces the zero map in Tate cohomology in all degrees. In an earlier paper we showed that the thick subcategory generated by the trivial module has no nonzero ghost maps if and only if the Sylow 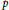$p$-subgroup of 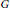$G$ is cyclic of order $2$ or $3$. In this paper we introduce and study variations of ghost maps. In particular, we consider the behavior of ghost maps under restriction and induction functors. We find all groups satisfying a strong form of Freyd’s generating hypothesis and show that ghosts can be detected on a finite range of degrees of Tate cohomology. We also consider maps that mimic ghosts in high degrees.

Keywords

20C2020J0655P42Tate cohomologyghost mapsstable module categoryalmost split sequenceperiodic cohomology
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 682 - 692
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aksu, E. A. and Green, D. J., On the Christensen-Wang bounds for the ghost number of a p-group algebra. arxiv:1502.05727Google Scholar
[2] Auslander, M. and Carlson, J. F.. Almost-split sequences and group rings. J. Algebra 103(1986), 122–140. http://dx.doi.Org/10.1016/0021-8693(86)90173-0 Google Scholar
[3] Benson, D. J., Representations and cohomology. I, II. Cambridge University Press, Cambridge, 1991.Google Scholar
[4] Benson, D. J. and Carlson, J. F., Products in negative cohomology. J. Pure Appl. Algebra, 82(1992), 107–129. http://dx.doi.Org/10.1016/0022-4049(92)90116-W Google Scholar
[5] Benson, D. J., Chebolu, S. K., Christensen, J. D., and Minac, J., The generating hypothesis for the stable module category of a p-group. J. Algebra 310(2007), 428–433. http://dx.doi.Org/10.1016/j.jalgebra.2006.12.013 Google Scholar
[6] Carlson, J. E., Modules and group algebras, (notes by Ruedi Suter) Lectures in Mathematics ETH Zurich. Birkhauser Verlag, Basel, 1996.Google Scholar
[7] Carlson, J. E., Chebolu, S. K., and Minac, J., Freyd's generating hypothesis with almost split sequences. Proc. Amer. Math. Soc. 137(2009), 2575–2580. http://dx.doi.Org/10.1090/S0002-9939-09-09826-8 Google Scholar
[8] Carlson, J. E., Chebolu, S. K., and Minac, J., Finite generation ofTate cohomology, Represent. Theory, 15(2011), 244–257. http://dx.doi.Org/10.1090/S1088-4165-2011-00385-X Google Scholar
[9] Carlson, J. E., Townsley, L., Valero-Elizondo, L., and Zhang, M., Cohomology rings of finite groups. Kluwer, Dordrecht, 2003.Google Scholar
[10] Chebolu, S. K., Christensen, J. D., and Minac, J., Ghosts in modular representation theory Adv. Math. 217(2008), 2782–2799. http://dx.doi.Org/10.1016/j.aim.2007.11.008 Google Scholar
[11] Chebolu, S. K., Christensen, J. D., and Minac, J., Groups which do not admit ghosts. Proc. Amer. Math. Soc. 136(2008), 1171–1179. http://dx.doi.Org/10.1090/S0002-9939-07-09058-2 Google Scholar
[12] Chebolu, S. K., Christensen, J. D., and Minac, J., Freyd's generating hypothesis for groups with periodic cohomology. Canad. Math. Bull. 55(2012), 48–59. http://dx.doi.Org/10.4153/CMB-2011-090-5 Google Scholar
[13] Christensen, J. D. and Wang, G., Ghost numbers of group algebras. Algebr. Represent. Theory 18(2015), 1–33. http://dx.doi.Org/10.1007/s10468-014-9476-9 Google Scholar
[14] Christensen, J. D. and Wang, G., Ghost numbers of group algebras. II. Algebr. Represent. Theory 18(2015), no. 3, 849–880. http://dx.doi.Org/10.1007/s10468-015-9519-x Google Scholar
[15] Freyd, P., Stable homotopy. Proc. Conf. Categorical Algebra (La Jolla, CA., 1965), Springer, New York, 1966, pp. 121–172.Google Scholar
[16] Heller, A. and Reiner, I., Indecomposable representations. Illinois J. Math. 5(1961), 314–323.Google Scholar
[17] Hovey, M., Lockridge, K. H., and Puninski, G., The generating hypothesis in the derived category of a ring. Math. Z. 256(2007), 789–800. http://dx.doi.Org/10.1007/s00209-007-0103-x Google Scholar
[18] Hovey, M., Lockridge, K. H., and Puninski, G., The ghost dimension of a ring. Proc. Amer. Math. Soc. 137(2009), 1907–1913. http://dx.doi.Org/10.1090/S0002-9939-09-09672-5 Google Scholar
[19] Hovey, M., Lockridge, K. H., and Puninski, G., The ghost and weak dimensions of rings and ring spectra. Israel J. Math. 182(2011), 31–46. http://dx.doi.Org/10.1007/s11856-011-0022-8 Google Scholar
[20] Lockridge, K. H., The generating hypothesis in the derived category of R-modules. J. Pure Appl. Algebra 208(2007), 485–495. http://dx.doi.Org/1 0.101 6/j.jpaa.2006.01.01 8 Google Scholar
[21] Webb, P. J.. The Auslander-Reiten quiver of a finite group. Math. Z. 179(1982), 97–121. http://dx.doi.Org/10.1007/BF01173918 Google Scholar