Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T20:24:34.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Perspective on Piecewise Polynomiality of Double Hurwitz Numbers

Published online by Cambridge University Press:  20 November 2018

Renzo Cavalieri  and
Steffen Marcus
Renzo Cavalieri
Affiliation:
Colorado State University, Department of Mathematics, Weber Building, Fort Collins, CO 80523, U.S.A e-mail: [email protected]
Steffen Marcus
Affiliation:
Department of Mathematics, University of Utah, E Room 233, Salt Lake City, UT 84112, U.S.A e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe double Hurwitz numbers as intersection numbers on the moduli space of curves 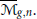${{\overline{M}}_{g,n}}$ Using a result on the polynomiality of intersection numbers of psi classes with the Double Ramification Cycle, our formula explains the polynomiality in chambers of double Hurwitz numbers and the wall-crossing phenomenon in terms of a variation of correction terms to the 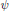$\varphi$ classes. We interpret this as suggestive evidence for polynomiality of the Double Ramification Cycle (which is only known in genera 0 and 1).

Keywords

14N35double Hurwitz numberswall crossingsmoduli spacesELSV formula
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 749 - 764
Copyright
Copyright © Canadian Mathematical Society 2014

References

[BCM13] Bertram, A., Cavalieri, R., and Markwig, H., Polynomiality, wall crossings and tropical geometry of rational double Hurwitz cycles.J. Combin. Theory Ser. A 120 (2013), no. 7, 1604–1631. http://dx.doi.org/10.1016/j.jcta.2013.05.010 Google Scholar
[BSSZ] Buryak, A., Shadrin, S., Spitz, L., and Zvonkine, D., Integrals of psi-classes over double ramification cycles. arxiv:1211.5273Google Scholar
[CJM11] Cavalieri, R., Johnson, P., and Markwig, H., Wall crossings for double Hurwitz numbers.Adv. Math. 228 (2011), no. 4, 1894–1937. http://dx.doi.org/10.1016/j.aim.2011.06.021 Google Scholar
[EGH00] Eliashberg, Y., Givental, A., and Hofer, H., Introduction to symplectic field theory.GAFA 2000 (Tel Aviv, 1999). Geom. Funct. Anal. 2000, Special Volume, Part II, 560–673.Google Scholar
[ELSV01] Ekedahl, T., Lando, S., Shapiro, M., and Vainshtein, A., Hurwitz numbers and intersections on moduli spaces of curves.Invent. Math. 146 (2001), no. 2, 297–327. http://dx.doi.org/10.1007/s002220100164 Google Scholar
[FP05] Faber, C. and Pandharipande, R., Relative maps and tautological classes.J. Eur. Math. Soc. (JEMS) 7 (2005), no. 1, 13–49. http://dx.doi.org/10.4171/JEMS/20 Google Scholar
[GJV05] Goulden, I. P., Jackson, D. M., and Vakil, R., Towards the geometry of double Hurwitz numbers.Adv. Math. 198 (2005), no. 1, 43–92. http://dx.doi.org/10.1016/j.aim.2005.01.008 Google Scholar
[GV03] Graber, T. and Vakil, R., Hodge integrals and Hurwitz numbers via virtual localization.Compositio Math. 135 (2003), no. 1, 25–36. http://dx.doi.org/10.1023/A:1021791611677 Google Scholar
[GV05] Graber, T. and Vakil, R., Relative virtual localization and vanishing of tautological classes on moduli spaces of curves.Duke Math. J. 130 (2005), no. 1, 1–37. http://dx.doi.org/10.1215/S0012-7094-05-13011-3 Google Scholar
[GZa] Grushevsky, S. and Zakharov, D., The double ramification cycle and the theta divisor. arxiv:1206.7001Google Scholar
[GZb] Grushevsky, S. and Zakharov, D., The zero section of the universal semiabelian variety, and the double ramification cycle. arxiv:1206.3534Google Scholar
[Hai11] Hain, R., Normal functions and the geometry of moduli spaces of curves. In: Handbook of moduli. I., Adv. Lect. Math. (ALM), Int. Press, Somervillw, MA, 2013, pp. 527–578.Google Scholar
[Has03] Hassett, B., Moduli spaces of weighted pointed stable curves. Adv. Math. 173 (2003), no. 2, 316–352. http://dx.doi.org/10.1016/S0001-8708(02)00058-0 Google Scholar
[Ion02] Ionel, E.-N., Topological recursive relations in H2g (Mg;n). Invent. Math. 148 (2002), no. 3, 627–658. http://dx.doi.org/10.1007/s002220100205 Google Scholar
[LM00] Losev, A. and Manin, Y., New moduli spaces of pointed curves and pencils of flat connections.Michigan Math. J. 48 (2000), 443–472. http://dx.doi.org/10.1307/mmj/1030132728 Google Scholar
[OP06] Okounkov, A. and Pandharipande, R., Gromov-Witten theory, Hurwitz theory, and completed cycles.Ann. of Math. (2) 163 (2006), no. 2, 517–560. http://dx.doi.org/10.4007/annals.2006.163.517 Google Scholar
[SSV08] Shadrin, S., Shapiro, M., and Vainshtein, A., Chamber behavior of double Hurwitz numbers in genus 0.Adv. Math. 217 (2008), no. 1, 79–96. http://dx.doi.org/10.1016/j.aim.2007.06.016 Google Scholar