Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-03T01:32:20.656Z Has data issue: false hasContentIssue false
  • English
  • Français

A Geometric Model for the Generalized Symmetric Group

Published online by Cambridge University Press:  20 November 2018

Norman W. Johnson
Norman W. Johnson*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalized symmetric group S(n, m) consists of all permutations of mn symbols commutative with

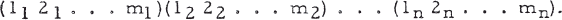
Since each cycle Qi = (1i 2i … mi) is of order m, there are mn permutations within the n cycles, generating an invariant subgroup Q of order mn. Also, there are n! ways of permuting the cycles among themselves, by transformations

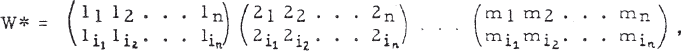
where i1, i2, …, in are the symbols 1, 2, …, n in some order [5, p. 39]. The permutations W* form a subgroup Sn* of order n!, isomorphic to the symmetric group Sn.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 3 , Issue 2 , 01 May 1960 , pp. 133 - 142
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Coxeter, H. S. M., The polytopes with regular-prismatic vertex figures, Philos. Trans. Roy. Soc. London Ser. A 229 (1930), 329-425.Google Scholar
2. Coxeter, H. S. M., The abstract groups Rm=Sm=(RjSj)Pj = l, sm=T2=(SJT)2Pj = l, and Sm=T2=(S-JTSJT)PJ=1, Proc. London Math. Soc. (2) 41 (1936), 278-301.Google Scholar
3. Coxeter, H. S. M., Regular Polytopes (London, 1948; New York, 1949).Google Scholar
4. Manning, H. P., Geometry of Four Dimensions (New York, 1914).Google Scholar
5. Osima, M., On the representations of the generalized symmetric group, Math. J. Okayama Univ. 4 (1954), 39-56.Google Scholar
6. Shephard, G. C., Regular complex polytopes, Proc. London Math. Soc. (3) 2 (1952), 82-97.Google Scholar
7. Shephard, G. C., Unitary groups generated by reflections, Canad. J. Math. 5 (1953), 364-383.Google Scholar
8. Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canad. J. Math. 6 (1954), 274-304.10.4153/CJM-1954-028-3Google Scholar