In a paper [1], published in 1990, in a (somewhat inaccessible) conference proceedings, the authors had shown that for the unitary operators on a separable Hilbert space, endowed with the strong operator topology, those with singular, continuous, simple spectrum, with full support, forma dense 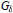${{G}_{\delta }}$. A similar theorem for bounded self-adjoint operators with a given normbound (omitting simplicity) was recently given by Barry Simon [2], [3], with a totally different proof. In this note we show that a slight modification of our argument, combined with the Cayley transform, gives a proof of Simon’s result, with simplicity of the spectrum added.