Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T15:41:51.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating Some Symmetric Semi-classical Orthogonal Polynomials

Published online by Cambridge University Press:  20 November 2018

Mohamed Zaatra
Mohamed Zaatra*
Affiliation:
Institut Supérieur des Sciences et Techniques des Eaux de Gabès, Campus universitaire, Gabès 6072, Tunisia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if $v$ is a regular semi-classical form (linear functional), then the symmetric form $u$ defined by the relation 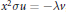${{x}^{2}}\sigma u\,=\,-\lambda v$, where 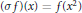$\left( \sigma f \right)\left( x \right)\,=\,f\left( {{x}^{2}} \right)$ and the odd moments of $u$ are 0, is also regular and semi-classical form for every complex $\lambda $ except for a discrete set of numbers depending on $v$. We give explicitly the three-term recurrence relation and the structure relation coefficients of the orthogonal polynomials sequence associated with $u$ and the class of the form $u$ knowing that of $v$. We conclude with an illustrative example.

Keywords

33C4542C05orthogonal polynomialsquadratic decompositionsemi-classical formsstructure relation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 877 - 890
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Alaya, J. and Maroni, P., Symmetric Laguerre-Hahn forms of class s = 1. Integral Transform. Spec. Fund. 4(1996), no. 4, 301–320. http://dx.doi.Org/10.1080/10652469608819117 Google Scholar
[2] Alaya, J. and Maroni, P., Semi-classical and Laguerre-Hahn forms defined by pseudo-functions. Methods Appl. Anal. 3(1996), no. 1, 12–30.Google Scholar
[3] Alvarez-Nodarse, R., Arvesû, J., and Marcellân, F., Modifications of quasi-definite linear functionals via addition of delta and derivatives of delta Dirac functions. Indag. Math. (N.S.) 15(2004), no. 1, 1–20. http://dx.doi.Org/10.1016/S0019-3577(04)90001-8 Google Scholar
[4] Beghdadi, D. and Maroni, P., On the inverse problem of the product of a form by a polynomial. J. Comput. Appl. Math. 88(1998), no. 2, 377–399. http://dx.doi.Org/10.1016/S0377-0427(97)00227-6 Google Scholar
[5] Bouras, B. and Alaya, A., A large family of semi-classical polynomials of class one. Integral Transforms Spec. Fund. 18(2007), no. 11-12, 913–931. http://dx.doi.Org/10.1080/10652460701511269 Google Scholar
[6] Chihara, T. S., An introduction to orthogonal polynomials. Mathematics and its Applications, 13, Gordon and Breach, New York, 1978.Google Scholar
[7] Chihara, T. S., On co-recursive orthogonal polynomials. Proc. Amer. Math. Soc. 8(1957), 899–905. http://dx.doi.Org/10.1090/S0002-9939-1957-0092015-5 Google Scholar
[8] Dini, J. and Maroni, P., Sur la multiplication d'une forme semi-classique par un polynôme. Publ. Sem. Math. Univ. d'Antananarivo 3(1989), 76–89.Google Scholar
[9] Kim, D. H., Kwon, K. H., and Park, S. B., Delta perturbation of a moment functional. Appl. Anal., 74(2000), no. 3-4, 463–477. http://dx.doi.Org/10.1080/00036810008840828 Google Scholar
[10] Kwon, K. H. and Park, S. B., Two point masses perturbation of quasi-define moment functionals. Indag. Math. (N.S.) 8(1997), no. 1, 79–93. http://dx.doi.Org/10.1016/S0019-3577(97)83352-6 Google Scholar
[11] Marcellân, F. and Maroni, P., Sur l'adjonction d'une masse de Dirac à une forme régulière et semi-classique. Ann. Mat. Pura Appl. (4) 162(1992), 1–22. http://dx.doi.Org/10.1007/BF01759996 Google Scholar
[12] Maroni, P. and Mejri, M., Some semi-classical orthogonal polynomials of class one. Eurasian Math. J. 2(2011), 108–128.Google Scholar
[13] Maroni, P. and Nicolau, I., On the inverse problem of product of a form by a monomial: the case n = 4. I. Integral Transforms Spec. Fund. 21(2010), no. 1-2, 35–56. http://dx.doi.Org/10.1080/10652460903016117 Google Scholar
[14] Maroni, P. and Nicolau, I., On the inverse problem of the product of a form by a polynomial: The cubic case. Appl. Numer. Math. 45(2003), no. 4, 419–451. http://dx.doi.Org/10.1016/S0168-9274(02)00250-7 Google Scholar
[15] Maroni, P., Variations around classical orthogonal polynomials. Connected problems. In: Proceedings of the Seventh Spanish Symposium on Orthogonal Polynomials and Applications (VII SPOA) (Granada, 1991), J. Comput. Appl. Math. 48(1993), no. 1-2, 133–155. http://dx.doi.Org/10.1016/0377-0427(93)90319-7 Google Scholar
[16] Maroni, P., Sur la décomposition quadratique d'une suite de polynômes orthogonaux. I. Riv. Mat. Pura Appl. 6(1990), 19–53.Google Scholar
[17] Maroni, P., Une théorie algébrique des polynômes orthogonaux. Application auxpolynômes orthogonaux semi-classiques. In: Orthogonal Polynomials and their applications (Erice, 1990), IMACS Ann. Comput. Appl. Math., 9, Baltzer, Basel. 1991, pp. 95–130.Google Scholar
[18] Maroni, P., Sur la suite de polynômes orthogonaux associée à la forme u = ôc + Mx — c)∼lL. Period. Math. Hungar. 21(1990), no. 3, 223–248. http://dx.doi.Org/10.1007/BF02651091 Google Scholar
[19] Sghaier, M. and Alaya, J., Orthogonal polynomials associated with some modifications of a linear form. Methods Appl. Anal. 11(2004), no. 2, 267–293.Google Scholar