No CrossRef data available.
Article contents
Generating Ideals in Rings of Integer-Valued Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 
$R$ be a one-dimensional locally analytically irreducible Noetherian domain with finite residue fields. In this note it is shown that if 
$I$ is a finitely generated ideal of the ring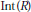 
$\text{Int(}R)$ of integer-valued polynomials such that for each 
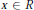$\text{x}\,\in \,R$ the ideal
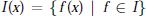$I\text{(}x\text{)}=\{f(x)|f\in I\}$ is strongly 
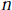$\text{n}$-generated, 
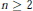$n\,\ge \,2$, then $I$ is 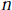$\text{n}$-generated, and some variations of this result.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
[1]
Brizolis, D., A theorem on ideals in Prüfer rings of integral-valued polynomials. Comm. Algebra 7 (1979), 1065–1077.Google Scholar
[2]
Cahen, P. J. and Chabert, J. L., Integer-valued polynomials. Math. SurveysMonographs 48, Amer.Math. Soc., Providence, Rhode Island, 1997.Google Scholar
[4]
Chabert, J. L., Invertible ideals of the ring of integral valued polynomials. Comm. Algebra 23 (1995), 4461–4471.Google Scholar
[5]
Gilmer, R., The n-generator property for commutative rings. Proc. Amer. Math. Soc. 38 (1973), 477–482.Google Scholar
[6]
Gilmer, R. and Smith, W. W., Finitely generated ideals in the ring of integer-valued polynomials. J. Algebra 81 (1983), 150–164.Google Scholar
[7]
Kunz, E., Introduction to commutative algebra and algebraic geometry. Birkhäuser, Boston, 1985.Google Scholar
[8]
Lazard, D. and Huet, P., Dominions des anneaux commutatifs. Bull. Sci. Math. Sér. 2 94 (1970), 193–199.Google Scholar
[9]
McQuillan, D. L., On Prüfer domains of polynomials. J. Reine. Angew.Math. 358 (1985), 162–178.Google Scholar
[10]
Ostrowski, A., Über ganzwertige polynome in algebraischen Zalkörpern. J. Reine. Angew. Math. 149 (1919), 117–124.Google Scholar
[11]
Polya, G., Über ganzwertige polynome in algebraischen Zalkörpern. J. Reine. Angew. Math. 149 (1919), 97–116.Google Scholar
[12]
Rush, D. E., Generating ideals in rings of integer-valued polynomials. J. Algebra 92 (1985), 389–394.Google Scholar
[13]
Rush, D. E., The conditions Int 
for integer-valued polynomials. J. Pure Appl. Algebra 125 (1998), 287–303.Google Scholar
for integer-valued polynomials. J. Pure Appl. Algebra 125 (1998), 287–303.Google Scholar[14]
Sally, J., Numbers of generators of ideals in local rings. Lecture Notes in Pure and Appl. Math. 35, Marcel Dekker, New York, 1978.Google Scholar
[15]
Skolem, Th., Einige Sätz über Polynome. Avh. Norske Vid. Akad. Oslo. 4 (1940), 1–16.Google Scholar
You have
Access