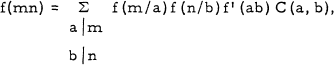Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-08T22:55:42.453Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating Functions for a Class of Arithmetic Functions

Published online by Cambridge University Press:  20 November 2018

A. A. Gioia  and
M.V. Subbarao
A. A. Gioia
Affiliation:
Texas Technological College and University of Alberta
M.V. Subbarao
Affiliation:
Texas Technological College and University of Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note the arithmetic functions L(n) and w(n) denote respectively the number and product of the distinct prime divisors of the integer n ≥ 1, and L(l) = 0, w(l) = 1. An arithmetic function f is called multiplicative if f(1) = 1 and f(mn) = f(m)f(n) whenever (m, n) = 1. It is known ([1], [3], [4]) that every multiplicative function f satisfies the identity

1.1

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 4 , October 1966 , pp. 427 - 431
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Gioia, A. A., On an identity for multiplicative functions, Amer. Math. Monthly 69, (1962), pages 988-991.Google Scholar
2. Subbarao, M.V., A generating function for a class of arithmetic functions. Amer. Math. Monthly 70, (1963), pages 841-842.Google Scholar
3. Vaidyanathaswamy, R., The identical equations of the multiplicative function. Bull. Amer. Math. Soc. 36, (1930), pages 762-772.Google Scholar
4. Vaidyanathaswamy, R., The theory of multiplicative arithmetic functions. Trans. Amer. Math. Soc. 33, (1931), pages 579-662.Google Scholar