The generating degree 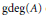$\text{g}\deg \left( A \right)$ of a topological commutative ring 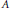$A$ with char 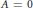$A\,=\,0$ is the cardinality of the smallest subset 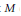$M$ of 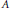$A$ for which the subring 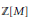$\mathbb{Z}\left[ M \right]$ is dense in 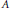$A$. For a prime number 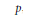$p$, 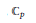${{\mathbb{C}}_{p}}$ denotes the topological completion of an algebraic closure of the field 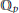${{\mathbb{Q}}_{p}}$ of 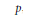$p$-adic numbers. We prove that 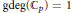$\text{g}\deg \left( {{\mathbb{C}}_{p}} \right)\,=\,1$, i.e., there exists $t$ in 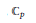${{\mathbb{C}}_{p}}$ such that 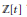$\mathbb{Z}\left[ t \right]$ is dense in 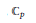${{\mathbb{C}}_{p}}$. We also compute 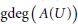$\text{gdeg}\left( A\left( U \right) \right)$ where 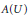$A\left( U \right)$ is the ring of rigid analytic functions defined on a ball 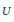$U$ in 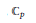${{\mathbb{C}}_{p}}$. If 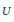$U$ is a closed ball then 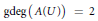$\text{gdeg}\left( A\left( U \right) \right)\,=\,2$ while if 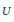$U$ is an open ball then 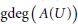$\text{gdeg}\left( A\left( U \right) \right)$ is infinite. We show more generally that 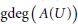$\text{gdeg}\left( A\left( U \right) \right)$ is finite for any affinoid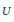$U$ in 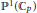${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$ and 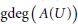$\text{gdeg}\left( A\left( U \right) \right)$ is infinite for any wide open subset 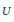$U$ of 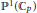${{\mathbb{P}}^{1}}\left( {{\mathbb{C}}_{p}} \right)$.