Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T09:57:05.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Goldberg Formula

Published online by Cambridge University Press:  20 November 2018

Antonio De Nicola  and
Ivan Yudin
Antonio De Nicola
Affiliation:
CMUC, Department of Mathematics, University of Coimbra, 3001-501 Coimbra, Portugal e-mail: [email protected] e-mail: [email protected]
Ivan Yudin
Affiliation:
CMUC, Department of Mathematics, University of Coimbra, 3001-501 Coimbra, Portugal e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove a useful formula for the graded commutator of the Hodge codifferential with the left wedge multiplication by a fixed 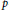$p$-form acting on the de Rham algebra of a Riemannian manifold. Our formula generalizes a formula stated by Samuel $\text{I}$. Goldberg for the case of 1-forms. As first examples of application we obtain new identities on locally conformally Kähler manifolds and quasi-Sasakian manifolds. Moreover, we prove that under suitable conditions a certain subalgebra of differential forms in a compact manifold is quasi-isomorphic as a 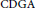$\text{CDGA}$ to the full de Rham algebra.

Keywords

53C2553D35graded commutatorHodge codifferentialHodge Laplaciande Rham cohomologylocally conformal Kaehler manifoldquasi-Sasakian manifold
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 3 , 01 September 2016 , pp. 508 - 520
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Boyer, C. P. and Galicki, K., Sasakian geometry. Oxford Mathematical Monographs, Oxford University Press, Oxford, 2008.Google Scholar
[2] Cappelletti-Montano, B., De Nicola, A., and Yudin, I., A survey on cosymplectic geometry.Rev. Math.Phys. 25(2013), no. 10, 1343002, 55.http://dx.doi.org/10.1142/S0129055X13430022 Google Scholar
[3] Cappelletti-Montano, B., De Nicola, A., and Yudin, I., Hard Lefschetz theorem for Sasakian manifolds. J. Differential Geom. 101(2015), no. 1, 47–66.Google Scholar
[4] Deligne, P., Griffiths, P., Morgan, J., and Sullivan, D., Real homotopy theory of Kâhler manifolds. Invent. Math. 29(1975), no. 3, 245–274. http://dx.doi.org/10.1007/BF01389853 Google Scholar
[5] Dragomir, S. and Ornea, L., Locally conformal Kähler geometry.Progress in Mathematics, 155, Birkhäuser Boston, Inc., Boston, MA, 1998. http://dx.doi.org/10.1007/978-1-4612-2026-8 Google Scholar
[6] Frölicher, A. Nijenhuis, A., Theory of vector-valued differential forms. I. Derivations of the graded ring of differential forms. Nederl.Akad.Wetensch.Proc. Ser. A. 59; Indag.Math. 18(1956), 338–359. http://dx.doi.org/10.1016/S1385-7258(56)50046-7 Google Scholar
[7] Frölicher, A. Nijenhuis, A., Some new cohomology invariants for complex manifolds. I. II. Nederl.Akad.Wetensch. Proc. Ser. A. 59; Indag.Math. 18(1956), 540–552, 553-564.Google Scholar
[8] Fujitani, T., Complex-valued differential forms on normal contact Riemannian manifolds. Tôhoku Math. J. (2) 18(1966), 349–361. http://dx.doi.org/10.2748/tmjV1178243376 Google Scholar
[9] Goldberg, S. I., Conformal transformations of Kaehler. Bull. Amer. Math. Soc. 66(1960), 54–58. http://dx.doi.org/10.1090/S0002-9904-1960-10390-4 Google Scholar
[10] Goldberg, S. I., Curvature and homology. Pure and Applied Mathematics, 11, Academic Press, New York-London, 1962.Google Scholar
[11] Kanemaki, S., Quasi-Sasakian manifolds. Tôhoku Math. J. 29(1977), no. 2, 227–233. http://dx.doi.org/! 0.2748/tmj/11 78240654 Google Scholar