Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-21T20:46:34.076Z Has data issue: false hasContentIssue false
  • English
  • Français

A Gap Principle for Subvarieties with Finitely Many Periodic Points

Part of: Arithmetic and non-Archimedean dynamical systems Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  28 February 2020

Keping Huang
Keping Huang*
Affiliation:
Department of Mathematics, University of Rochester, Rochester, NY 14627, USA Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 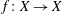$f:X\rightarrow X$ be a quasi-finite endomorphism of an algebraic variety 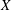$X$ defined over a number field 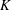$K$ and fix an initial point 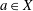$a\in X$. We consider a special case of the Dynamical Mordell–Lang Conjecture, where the subvariety 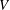$V$ contains only finitely many periodic points and does not contain any positive-dimensional periodic subvariety. We show that the set 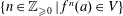$\{n\in \mathbb{Z}_{{\geqslant}0}\mid f^{n}(a)\in V\}$ satisfies a strong gap principle.

Keywords

dynamical Mordell-Lang conjecturegap principle

MSC classification

Primary: 37P05: Polynomial and rational maps
Secondary: 37P55: Arithmetic dynamics on general algebraic varieties 11S82: Non-Archimedean dynamical systems 37P35: Arithmetic properties of periodic points
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 382 - 392
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J., A generalised Skolem–Mahler–Lech theorem for affine varieties. J. London Math. Soc. (2) 73(2006), 367–379.10.1112/S002461070602268XCrossRefGoogle Scholar
Benedetto, R., Ghioca, D., Hutz, B., Kurlberg, P., Scanlon, T., and Tucker, T., Periods of rational maps modulo primes. Math. Ann. 355(2013), 637–660.Google Scholar
Benedetto, R., Ghioca, D., Kurlberg, P., and Tucker, T., A gap principle for dynamics. Compos. Math. 146(2010), 1056–1072.10.1112/S0010437X09004667CrossRefGoogle Scholar
Benedetto, R., Ghioca, D., Kurlberg, P., and Tucker, T., A case of the dynamical Mordell–Lang conjecture. Math. Ann. 352(2012), 1–26. Appendix by Umberto Zannier.Google Scholar
Bell, J., Ghioca, D., and Tucker, T., The dynamical Mordell–Lang problem for étale maps. Amer. J. Math. 132(2010), 1655–1675.Google Scholar
Bell, J., Ghioca, D., and Tucker, T., Applications of p-adic analysis for bounding periods for subvarieties under étale maps. Int. Math. Res. Not. IMRN 2015(2015), 11, 3576–3597.Google Scholar
Bell, J., Ghioca, D., and Tucker, T., The dynamical Mordell–Lang problem for Noetherian spaces. Funct. Approx. Comment. Math. 53(2015), 313–328.10.7169/facm/2015.53.2.7CrossRefGoogle Scholar
Bell, J., Ghioca, D., and Tucker, T. J., The dynamical Mordell–Lang conjecture. Math. Surveys Monogr., 210, American Mathematical Society, Providence, RI, 2016.CrossRefGoogle Scholar
Cohen, I., On the structure and ideal theory of complete local rings. Trans. Amer. Math. Soc. 59(1946), 54–106.10.1090/S0002-9947-1946-0016094-3CrossRefGoogle Scholar
Denis, L., Géométrie diophantienne sur les modules de Drinfel’d. In: The arithmetic of function fields (Columbus, OH, 1991). Ohio State Univ. Math. Res. Inst. Publ., 2, de Gruyter, Berlin, 1992, pp. 285–302.Google Scholar
Davenport, H. and Roth, K., Rational approximations to algebraic numbers. Mathematika 2(1955), 160–167.10.1112/S0025579300000814CrossRefGoogle Scholar
Fakhruddin, N., Questions on self maps of algebraic varieties. J. Ramanujan Math. Soc. 18(2003), 109–122.Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Invent. Math. 73(1983), 349–366.CrossRefGoogle Scholar
Ghioca, D., Nguyen, K., and Ye, H., The dynamical Manin–Mumford conjecture and the dynamical Bogomolov conjecture for endomorphisms of (ℙ1)n. Compos. Math. 154(2018), 1441–1472.10.1112/S0010437X18007157CrossRefGoogle Scholar
Ghioca, D., Nguyen, K., and Ye, H., The dynamical Manin–Mumford conjecture and the dynamical Bogomolov conjecture for split rational maps. J. Eur. Math. Soc. (JEMS) 21(2019), 1571–1594.CrossRefGoogle Scholar
Ghioca, D. and Tucker, T., Periodic points, linearizing maps, and the dynamical Mordell–Lang problem. J. Number Theory 129(2009), 1392–1403.10.1016/j.jnt.2008.09.014CrossRefGoogle Scholar
Guralnick, R., Tucker, T., and Zieve, M., Exceptional covers and bijections on rational points. Int. Math. Res. Not. IMRN 2007(2007), Art. ID rnm004, 20.Google Scholar
Ghioca, D., Tucker, T., and Zhang, S., Towards a dynamical Manin–Mumford conjecture. Int. Math. Res. Not. IMRN 2011(2011), 5109–5122.Google Scholar
Hartshorne, R., Algebraic geometry. In: Graduate Texts in Math., Vol. 52. Springer–Verlag, New York–Heidelberg, 1977.Google Scholar
Matsumura, H., Commutative ring theory. Cambridge Stud. Adv. Math., 8, Cambridge University Press, Cambridge, 1986. (translated from the Japanese by M. Reid).Google Scholar
Mumford, D., A remark on Mordell’s conjecture. Amer. J. Math. 87(1965), 1007–1016.10.2307/2373258CrossRefGoogle Scholar
Xie, J., The dynamical Mordell–Lang conjecture for polynomial endomorphisms of the affine plane. Astérisque 394(2017), vi+110.Google Scholar
Zhang, S., Small points and adelic metrics. J. Algebraic Geom. 4(1995), 281–300.Google Scholar
Zhang, S., Distributions in algebraic dynamics. In: Surveys in differential geometry, Vol. X. Surv. Differ. Geom., 10, International Press, Somerville, MA, 2006, pp. 381–430.Google Scholar