Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T04:21:29.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois Groups of Even Sextic Polynomials

Part of: Field extensions Computational number theory

Published online by Cambridge University Press:  12 December 2019

Chad Awtrey  and
Peter Jakes
Chad Awtrey
Affiliation:
Department of Mathematics and Statistics, Elon University, Campus Box 2320, Elon, NC 27244 Email: [email protected]@elon.edu
Peter Jakes
Affiliation:
Department of Mathematics and Statistics, Elon University, Campus Box 2320, Elon, NC 27244 Email: [email protected]@elon.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 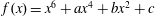$f(x)=x^{6}+ax^{4}+bx^{2}+c$ be an irreducible sextic polynomial with coefficients from a field 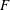$F$ of characteristic 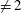$\neq 2$, and let 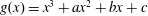$g(x)=x^{3}+ax^{2}+bx+c$. We show how to identify the conjugacy class in 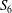$S_{6}$ of the Galois group of $f$ over 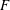$F$ using only the discriminants of 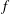$f$ and $g$ and the reducibility of a related sextic polynomial. We demonstrate that our method is useful for producing one-parameter families of even sextic polynomials with a specified Galois group.

Keywords

even polynomialssexticGalois group

MSC classification

Primary: 11Y40: Algebraic number theory computations
Secondary: 12F10: Separable extensions, Galois theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 670 - 676
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Butler, G. and McKay, J., The transitive groups of degree up to eleven. Comm. Algebra 11(1983), no. 8, 863–911. https://doi.org/10.1080/00927878308822884CrossRefGoogle Scholar
Cohen, H., A course in computational algebraic number theory. Graduate Texts in Mathematics, 138, Springer-Verlag, Berlin, 1993. https://doi.org/10.1007/978-3-662-02945-9CrossRefGoogle Scholar
Eloff, D., Spearman, B. K., and Williams, K. S., A 4-sextic fields with a power basis. Missouri J. Math. Sci. 19(2007), no. 3, 188–194.10.35834/mjms/1316032976Google Scholar
Harrington, J. and Jones, L., The irreducibility of power compositional sextic polynomials and their Galois groups. Math. Scand. 120(2017), no. 2, 181–194. https://doi.org/10.7146/math.scand.a-25850CrossRefGoogle Scholar
Ide, J. and Jones, L., Infinite families of A 4-sextic polynomials. Canad. Math. Bull. 57(2014), no. 3, 538–545. https://doi.org/10.4153/CMB-2014-008-1CrossRefGoogle Scholar
Kappe, L.-C. and Warren, B., An elementary test for the Galois group of a quartic polynomial. Amer. Math. Monthly 96(1989), no. 2, 133–137. https://doi.org/10.2307/2323198CrossRefGoogle Scholar
Smith, G. W., Some polynomials over Q (t) and their Galois groups. Math. Comp. 69(2000), no. 230, 775–796. https://doi.org/10.1090/S0025-5718-99-01160-6CrossRefGoogle Scholar
Soicher, L., The computation of Galois groups. Master’s thesis, Concordia University, Montreal, 1981.Google Scholar