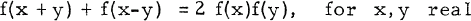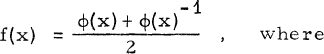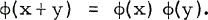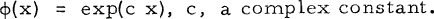Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Etigson, L. B.
1974.
A Cosine Functional Equation with Restricted Argument.
Canadian Mathematical Bulletin,
Vol. 17,
Issue. 4,
p.
505.
Perkins, Allison M.
and
Sahoo, Prasanna K.
2015.
On two functional equations with involution on groups related to sine and cosine functions.
Aequationes mathematicae,
Vol. 89,
Issue. 5,
p.
1251.
Zeglami, D.
and
Fadli, B.
2016.
Integral functional equations on locally compact groups with involution.
Aequationes mathematicae,
Vol. 90,
Issue. 5,
p.
967.
Belaid, B.
and
Elhoucien, E.
2016.
An extension of Van Vleck’s functional equation for the sine.
Acta Mathematica Hungarica,
Vol. 150,
Issue. 1,
p.
258.
Perkins, Allison M.
and
Sahoo, Prasanna K.
2016.
A functional equation with involution related to the cosine function.
Aequationes mathematicae,
Vol. 90,
Issue. 1,
p.
123.
Stetkær, Henrik
2017.
Kannappan’s functional equation on semigroups with involution.
Semigroup Forum,
Vol. 94,
Issue. 1,
p.
17.
Elhoucien, Elqorachi
2017.
Integral Van Vleck’s and Kannappan’s functional equations on semigroups.
Aequationes mathematicae,
Vol. 91,
Issue. 1,
p.
83.
Fadli, B.
Zeglami, D.
and
Kabbaj, S.
2018.
Solution of several functional equations on abelian groups with involution.
Afrika Matematika,
Vol. 29,
Issue. 1-2,
p.
1.
Belfakih, Keltouma
Elqorachi, Elhoucien
and
Redouani, Ahmed
2019.
Mathematical Analysis and Applications.
Vol. 154,
Issue. ,
p.
319.
Sabour, K. H.
Charifi, A.
and
Kabbaj, S.
2019.
Frontiers in Functional Equations and Analytic Inequalities.
p.
93.
Dimou, Hajira
Chahbi, Abdellatif
and
Kabbaj, Samir
2019.
A new generalization of Wilson’s functional equation.
Proyecciones (Antofagasta),
Vol. 38,
Issue. 5,
p.
943.
Ng, Che Tat
Zhao, Hou Yu
and
Lin, Xia
2020.
A functional equation on groups with involutions.
Aequationes mathematicae,
Vol. 94,
Issue. 3,
p.
511.
Ayoubi, Mohamed
and
Zeglami, Driss
2020.
D’Alembert’s Functional Equations on Monoids with an Anti-endomorphism.
Results in Mathematics,
Vol. 75,
Issue. 2,
Chahbi, Abdellatif
and
Elqorachi, Elhoucien
2022.
A Variant of d’Alembert Functional Equation on Monoids.
Bulletin of the Iranian Mathematical Society,
Vol. 48,
Issue. 3,
p.
1127.
Aserrar, Youssef
and
Elqorachi, Elhoucien
2024.
An extension of Kannappan’s functional equation on semigroups.
Semigroup Forum,
Vol. 109,
Issue. 2,
p.
222.
Ahmed, Jafar
Omar, Ajebbar
and
Elhoucien, Elqorachi
2024.
A Kannappan-sine addition law on semigroups.
Aequationes mathematicae,
Vol. 98,
Issue. 4,
p.
1001.
Jafar, Ahmed
Ajebbar, Omar
and
Elqorachi, Elhoucien
2024.
A Kannappan-sine subtraction law on semigroups.
Aequationes mathematicae,
Ouhabi, Ayoub
Zeglami, Driss
and
Ayoubi, Mohamed
2024.
Van Vleck’s and Kannappan’s functional equations for division ring-valued functions.
Semigroup Forum,
Vol. 109,
Issue. 3,
p.
669.
Ayoubi, Mohamed
and
Zeglami, Driss
2024.
A Functional Equation for the Cosine on Semigroups with Endomorphisms.
Vietnam Journal of Mathematics,
Vol. 52,
Issue. 1,
p.
149.
Aserrar, Y.
and
Elqorachi, E.
2024.
Kannappan–Wilson and Van Vleck–Wilson functional equations on semigroups.
Acta Mathematica Hungarica,
Vol. 173,
Issue. 1,
p.
193.