Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T20:46:46.927Z Has data issue: false hasContentIssue false
  • English
  • Français

The π-Full Tight Riesz Orders on A(Ω)

Published online by Cambridge University Press:  20 November 2018

Gary Davis  and
Stephen H. McCleary
Gary Davis
Affiliation:
La Trobe University, Bundoora, Victoria, Australia., University of Georgia, Athens, Georgia, USA
Stephen H. McCleary
Affiliation:
La Trobe University, Bundoora, Victoria, Australia., University of Georgia, Athens, Georgia, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a lattice-ordered group (l-group), and let t, u∈ G+. We write tπu if t ∧ g = 1 is equivalent to u ∧ g = 1, and say that a tight Riesz order T on G is π-full if t ∈ T and t π U imply u∈T. We study the set 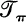of π-full tight Riesz orders on an l-permutation group (G, Ω), Ω a totally ordered set.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 24 , Issue 2 , 01 June 1981 , pp. 137 - 151
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Ball, R., Normal subgroups of the lattice-ordered group of automorphisms of the long line, to appear.Google Scholar
2. Ball, R., Which I-groups support a tight Riesz order? Google Scholar
3. Conrad, P., Lattice-ordered groups, Tulane University.Google Scholar
4. Cornish, W. H., Annulets and a-ideals in distributive lattices, J. Aust. Math. Soc.. 15 (1973), 70-77.Google Scholar
5. Davis, G. and Fox, C. D., Compatible tight Riesz orders on the group of automorphisms of an 0- 2-homogeneous set, Canad. J. Math.. 28 (1973), 1076-1081.Google Scholar
6. Ball, R., Compatible tight Riesz orders on the group of automorphisms of an 0-2-homogeneous set: Addendum, Canad. J. Math.. 29 (1977), 664-665.Google Scholar
7. Glass, A. M. W., Ordered permutation groups, Bowling Green State University, Bowling Green, Ohio, 1976.Google Scholar
8. Glass, A. M. W., Compatible tight Riesz orders, Canad. J. Math.. 28 (1976), 186-200.Google Scholar
9. Glass, A. M. W., Compatible tight Riesz orders II, Canad. J. Math.. 31 (1979), 304-307.Google Scholar
10. Holland, C., The lattice-ordered group of automorphisms of an ordered set, Michigan Math. J.. 10 (1963), 399-408.Google Scholar
11. Holland, C., A class of simple lattice-ordered permutation groups, Proc. Amer. Math. Soc.. 16 (1965), 326-329.Google Scholar
12. Lloyd, J. T., Complete distributive in certain infinite permutation groups, Michigan Math. J.. 14 (1967), 393-400.Google Scholar
13. Keimel, K., A unified theory of minimal prime ideals. Acta. Math. Acad. Sci. Hungar.. 23 (1972), 51-69.Google Scholar
14. McCleary, S. H., o-primitive ordered permutation groups, Pacific J. Math.. 40 (1972), 349-372.Google Scholar
15. McCleary, S. H., o-primitive ordered permutation groups II, Pacific J. Math.. 49 (1973), 431-443.Google Scholar
16. Reilly, N. R., Compatible tight Riesz orders and prime subgroups, Glasgow Math. J.. 14 (1973), 145-160.Google Scholar
17. Spirason, G. and Strzelecki, E., A note on Pt-ideals, J. Aust. Math. Soc.. 14 (1972), 304-310.Google Scholar