Let 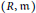$(R,\mathfrak{m})$ denote a local Cohen–Macaulay ring and $I$ a non-nilpotent ideal of $R$. The purpose of this article is to investigate Faltings’ finiteness dimension 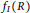${{f}_{I}}(R)$ and the equidimensionalness of certain homomorphic images of $R$. As a consequence we deduce that 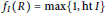${{f}_{I}}(R)=\max \{1,\text{ht}I\}$, and if 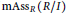$\text{mAs}{{\text{s}}_{R}}(R/I)$ is contained in 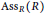$\text{As}{{\text{s}}_{R}}(R)$, then the ring 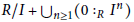$R/I+{{\bigcup }_{n\ge 1}}(0{{:}_{R}}{{I}^{n}})$ is equidimensional of dimension dim 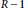$R-1$. Moreover, we will obtain a lower bound for injective dimension of the local cohomology module 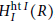$H_{I}^{\text{ht}I}(R)$, in the case where 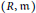$(R,\mathfrak{m})$ is a complete equidimensional local ring.