Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T16:42:26.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Factorized Groups with max, min and min-p

Published online by Cambridge University Press:  20 November 2018

Bernhard Amberg
Bernhard Amberg*
Affiliation:
Fachbereich Mathematik, Universität MainzD-6500 Mainz, West Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 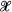be a class of groups which is closed under the forming of subgroups, epimorphic images and extensions. It is shown that every soluble product G = AB of two 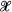-subgroups A and B, one of which satisfies max or min, is an 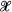-group (Theorem A). If X satisfies an additional requirement, then every soluble product G = AB of two 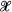-subgroups A and B, one of which is a torsion group with min-p for every prime p, is an 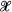-group (Theorem B). Corollary: Every soluble product G = AB of two π-subgroups A and B with min-p for every prime p in the set of primes π, is a π -group with min-p for every p.

Keywords

20 E 22 (also 20 F 16)
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 2 , 01 June 1984 , pp. 171 - 178
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Amberg, B., Artinian and noetherian factorized groups, Rend. Mat. Univ. Padova 55 (1976), 105–122.Google Scholar
2. Amberg, B., Factorizations of infinite soluble groups, Rocky Mountain J. of Math. 7 (1977), 1–17.Google Scholar
3. Amberg, B., Soluble products of two locally finite groups with min-p for every prime p, Rend. Mat. Univ. Padova 69 (1982) (3), 7–17.Google Scholar
4. Cernikov, N. S., Factorizations of locally finite groups, Sibir. Mat. J. 21 (1981), 830–897.Google Scholar
5. Kegel, O. H. and Wehrfritz, B. A. F., Locally finite groups, North-Holland, Amsterdam (1973).Google Scholar
6. J. Lennox and Roseblade, J., Soluble products of polycyclic groups, Math. Z. 110 (1980), 153–154.Google Scholar
7. Robinson, D. J. S., A course in the Theory of groups, Springer, New York, Heidelberg, Berlin (1980).Google Scholar
8. Zaicev, D. I., Products of abelian groups, Algebra and Logika 19 (1980), 150–172, Algebra and Logika 19 (1980), 94–106.Google Scholar
9. Zaicev, D. I., Products ofpolycyclic groups, Mat. Zametki 29 (1981), 481–490, Math. Notes 29 (1981), 247–252.Google Scholar