Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T04:23:51.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Values of

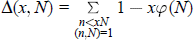
Published online by Cambridge University Press:  20 November 2018

P. Codecà  and
M. Nair
P. Codecà
Affiliation:
Dipartimento di Matematica Università di Ferrara via Machiavelli 35 44100 Ferrara Italy, e-mail: [email protected]
M. Nair
Affiliation:
Department of Mathematics University of Glasgow Glasgow G12 8QW UK, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The function 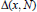$\Delta (x,N)$ as defined in the title is closely associated via 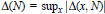$\Delta \,(N)\,=\,{{\sup }_{x}}\,|\,\Delta (x,N)|$ to several problems in the upper bound sieve. It is also known via a classical theorem of Franel that certain conjectured bounds involving averages of 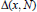$\Delta (x,N)$ are equivalent to the Riemann Hypothesis. We improve the unconditional bounds which have been hitherto obtained for 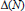$\Delta (N)$ and show that these are close to being optimal. 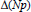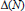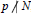Several auxiliary results relating $\Delta (Np)$ to $\Delta (N)$, where $p$ is a prime with $p\nmid N$, are also obtained and two new conjectures stated.

Keywords

11N25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 3 , 01 September 1998 , pp. 335 - 347
Copyright
Copyright © Canadian Mathematical Society 1998

References

[1] Delange, H., Sur la distribution des fractions irréductibles de dénominateur n ou de dénominateur au plus égalà x. In: Hommage au Professeur Lucien Godeaux. Centre Belge de Recherches Mathématiques, Louvain, 1968, 75–89.Google Scholar
[2] Erdös, P., Some remarks on a paper of McCarthy. Canad. Math. Bull. (2) 1 (1958), 71–75.Google Scholar
[3] Erdös, P., Remarks and corrections to my paper “Some remarks on a paper of McCarthy“. Canad.Math. Bull. (2) 3 (1960), 127–129.Google Scholar
[4] Franel, J., Les suites de Farey et les problèms des nombres premiers. Göttinger Nachr., 1924, 198–201.Google Scholar
[5] Landau, E., Vorlesungen über Zahlentheorie. Band 2, Teil 7, Kapitel 13. Chelsea, New York, 1950.Google Scholar
[6] Lehmer, D. H., The Distribution of Totatives. Canad. J. Math. 7 (1955), 347–357.Google Scholar
[7] McCarthy, P. J., Note on the distribution of the totatives. Amer. Math. Monthly 64 (1957), 585–586.Google Scholar
[8] Perelli, A. and Zannier, U., An extremal property of the Möbius function. Arch.Math. 53 (1989), 20–29.Google Scholar
[9] Suryanarayana, D., On Δ(x, n) = φ(x, n) − xφ(n)/n . Proc. Amer. Math. Soc. (1) 44 (1974), 17–21.Google Scholar
[10] Hamme, L. van, Sur une généralisation de l’indicateur d’Euler. Acad. Roy. Belg. Bull Cl. Sci. Sér. 5 57 (1971), 805–817.Google Scholar
[11] Vijayaraghavan, T., On a problem in elementary number theory. J. Indian Math. Soc. 15 (1951), 51–56.Google Scholar