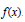Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Akande, Agbolade
2025.
Uniform distribution of polynomially-defined additive functions to varying moduli.
International Journal of Number Theory,
Vol. 21,
Issue. 04,
p.
959.