Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T03:15:12.184Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential Estimates for the Conjugate Function on Locally Compact Abelian Groups

Published online by Cambridge University Press:  20 November 2018

Nakhlé Habib Asmar
Nakhlé Habib Asmar*
Affiliation:
Department of Mathematics, University of Missouri-Columbia, Columbia, Missouri 65211 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact Abelian group, with character group X. Suppose that X contains a measurable order P. For 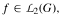the conjugate function of f is the function 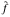whose Fourier transform satisfies the identity 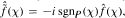for almost all χ in X where sgnp(χ) = - 1 , 0, 1, according as 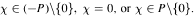We prove that, when f is bounded with compact support, the conjugate function satisfies some weak type inequalities similar to those of the Hilbert transform of a bounded function with compact support in ℝ. As a consequence of these inequalities, we prove that 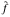possesses strong integrability properties, whenever f is bounded and G is compact. In particular, we show that, when G is compact and f is continuous on G, the function 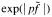is integrable for all p > 0.

Keywords

43A17
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 33 , Issue 1 , 01 March 1990 , pp. 34 - 44
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Nakhlé, Asmar. The conjugate function on the finite dimensional torus. Can. Math. Bull. Vol. 32 (2), 1989 (to appear).Google Scholar
2. Nakhlé, Asmar, Earl Berkson, and T. Alastair Gillespie, Representations of groups with ordered dual groups and generalized analyticity, J. Funct. Anal, (to appear).Google Scholar
3. Nakhlé, Asmar, and Hewitt, Edwin. Marcel Riesz's theorem on conjugate functions and its descendants. Proceedings of the Analysis Conference (Singapore, 1986), edited by S. T. L. Choy et al., Elsevier Science Publishers, New York, 1988, pp. 1–56.Google Scholar
4. Nakhlé, Asmar, A generalized M. Riesz theorem on conjugate functions, in “ Analysis at Urbana”, Vol. 1. Edited by Berkson, E., Peck, N. T., and J. J. Uhl. London Math. Soc. Lecture Note Series 137, Cambridge Univ. Press, 1989, pp. 41–46.Google Scholar
5. Alberto, Calderon. Ergodic theory and translation invariant operators. Proc. Nat. Acad. Sci. U.S.A. 59 (2), 1968, 349–353.Google Scholar
6. Ronald, Coifman, and Guido Weiss. Transference methods in analysis. Regional conference in Math., 31, Amer. Mat. Soc, Providence 1977.Google Scholar
7. Adriano, Garsia. Topics in almost everywhere convergence. Markham Publishing Company. Chicago 1970.Google Scholar
8. Hewitt, Edwin, and Gunter Ritter. Conjugate Fourier series on certain solenoids.Trans. Amer. Math. Soc. 276 (1983), 817–840 9. Hewitt, Edwin, and Kenneth Ross. Abstract Harmonic Analysis I.Grundlehren der mathematischen Wissenschaften, 115, Second Edition. Springer-Verlag, 1970.Google Scholar
10. Hewitt, Edwin, and Stromberg, Karl. Real and Abstract Analysis. Graduate Texts in Mathematics. Springer-Verlag, 1965.Google Scholar
11. Zygmund, Antoni. Trigonometric Series I and II. Cambridge University Press. Second Edition, 1959.Google Scholar