Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-09T20:22:43.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions of the Real Field by Canonical Products

Part of: Model theory Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  04 October 2019

Chris Miller  and
Patrick Speissegger
Chris Miller
Affiliation:
Department of Mathematics, Ohio State University, 231 West 18th Avenue, Columbus, Ohio43210, USA Email: [email protected]
Patrick Speissegger
Affiliation:
Department of Mathematics & Statistics, McMaster University, 1280 Main Street West, Hamilton, Ontario, L8S 4K1 Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider expansions of o-minimal structures on the real field by collections of restrictions to the positive real line of the canonical Weierstrass products associated with sequences such as 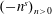$(-n^{s})_{n>0}$ (for 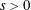$s>0$) and 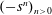$(-s^{n})_{n>0}$ (for 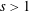$s>1$), and also expansions by associated functions such as logarithmic derivatives. There are only three possible outcomes known so far: (i) the expansion is o-minimal (that is, definable sets have only finitely many connected components); (ii) every Borel subset of each 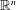$\mathbb{R}^{n}$ is definable; (iii) the expansion is interdefinable with a structure of the form 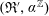$(\mathfrak{R}^{\prime },\unicode[STIX]{x1D6FC}^{\mathbb{Z}})$ where 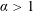$\unicode[STIX]{x1D6FC}>1$, 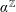$\unicode[STIX]{x1D6FC}^{\mathbb{Z}}$ is the set of all integer powers of $\unicode[STIX]{x1D6FC}$, and 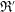$\mathfrak{R}^{\prime }$ is o-minimal and defines no irrational power functions.

Keywords

o-minimald-minimalAssouad dimensionWeierstrass productGevrey asymptotics

MSC classification

Primary: 03C64: Model theory of ordered structures; o-minimality
Secondary: 30D10: Representations of entire functions by series and integrals 30D15: Special classes of entire functions and growth estimates 30D60: Quasi-analytic and other classes of functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 3 , September 2020 , pp. 506 - 521
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of author C. M. partially supported by the Simons Foundation and by the Mathematisches Forschungsinstitut Oberwolfach (MFO). Research of author P. S. supported by NSERC of Canada Discovery Grant RGPIN 261961 and the Zukunftskolleg of the University of Konstanz. Preliminary versions of many of the results herein were announced by Miller at the Fields Institute for Research in Mathematical Sciences (August 2016) and at MFO (April–May 2017).

References

Balser, W., Formal power series and linear systems of meromorphic ordinary differential equations. Universitext, Springer-Verlag, New York, 2000.Google Scholar
Bank, S. B., On certain canonical products which cannot satisfy algebraic differential equations. Funkcial. Ekvac. 23(1980), 335–349.Google Scholar
Bank, S. B. and Kaufman, R. P., An extension of Hölder’s theorem concerning the Gamma function. Funkcial. Ekvac. 19(1976), 53–63.Google Scholar
Barnes, E. W., The asymptotic expansion of integral functions of finite non-zero order. Proc. London Math. Soc. (2) 3(1905), 273–295. https://doi.org/10.1112/plms/s2-3.1.273CrossRefGoogle Scholar
Dries, L. van den, Dense pairs of o-minimal structures. Fund. Math. 157(1998), 61–78.CrossRefGoogle Scholar
Dries, L. van den, Macintyre, A., and Marker, D., Logarithmic-exponential power series. J. London Math. Soc. (2) 56(1997), 417–434. https://doi.org/10.1112/S0024610797005437CrossRefGoogle Scholar
van den Dries, L. and Miller, C., Geometric categories and o-minimal structures. Duke Math. J. 84(1996), 497–540. https://doi.org/10.1215/S0012-7094-96-08416-1CrossRefGoogle Scholar
Dries, L. van den and Speissegger, P., The real field with convergent generalized power series. Trans. Amer. Math. Soc. 350(1998), 4377–4421. https://doi.org/10.1090/S0002-9947-98-02105-9CrossRefGoogle Scholar
van den Dries, L. and Speissegger, P., The field of reals with multisummable series and the exponential function. Proc. London Math. Soc. (3) 81(2000), 513–565. https://doi.org/10.1112/S0024611500012648.CrossRefGoogle Scholar
Ford, W. B., Studies on divergent series and summability and the asymptotic developments of functions defined by Maclaurin series. Chelsea Publishing Co., New York, 1960.Google Scholar
Friedman, H. and Miller, C., Expansions of o-minimal structures by fast sequences. J. Symbolic Logic 70(2005), 410–418. https://doi.org/10.2178/jsl/1120224720CrossRefGoogle Scholar
Hieronymi, P., Defining the set of integers in expansions of the real field by a closed discrete set. Proc. Amer. Math. Soc. 138(2010), 2163–2168. https://doi.org/10.1090/S0002-9939-10-10268-8CrossRefGoogle Scholar
Hieronymi, P., Expansions of subfields of the real field by a discrete set. Fund. Math. 215(2011), 167–175. https://doi.org/10.4064/fm215-2-4CrossRefGoogle Scholar
Hieronymi, P. and Miller, C., Metric dimensions and tameness in expansions of the real field. Trans. Amer. Math. Soc. 373(2020), 849–874. https://doi.org/10.1090/tran/7691CrossRefGoogle Scholar
Kechris, A. S., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4612-4190-4CrossRefGoogle Scholar
Kuhlmann, F.-V. and Kuhlmann, S., Valuation theory of exponential Hardy fields. I. Math. Z. 243(2003), 671–688. https://doi.org/10.1007/s00209-002-0460-4CrossRefGoogle Scholar
Littlewood, J. E., On the asymptotic approximation to integral functions of zero order. Proc. London Math. Soc. (2) 5(1907), 361–410. https://doi.org/10.1112/plms/s2-5.1.361CrossRefGoogle Scholar
Marker, D. and Miller, C., Levelled o-minimal structures. Real algebraic and analytic geometry (Segovia, 1995). Rev. Mat. Univ. Complut. Madrid 10(1997), 241–249.Google Scholar
Miller, C., Tameness in expansions of the real field. In: Logic Colloquium ’01. Lect. Notes Log., 20, Assoc. Symbol. Logic, Urbana, IL, 2005, pp. 281–316. https://doi.org/10.1017/9781316755860.012Google Scholar
Miller, C., Avoiding the projective hierarchy in expansions of the real field by sequences. Proc. Amer. Math. Soc. 134(2006), 1483–1493. https://doi.org/10.1090/S0002-9939-05-08112-8Google Scholar
Miller, C., Expansions of o-minimal structures on the real field by trajectories of linear vector fields. Proc. Amer. Math. Soc. 139(2011), 319–330. https://doi.org/10.1090/S0002-9939-2010-10506-3CrossRefGoogle Scholar
Miller, C., Basics of o-minimality and Hardy fields. In: Lecture notes on o-minimal structures and real analytic geometry. Fields Inst. Commun., 62, Springer, New York, 2012, pp. 43–69. https://doi.org/10.1007/978-1-4614-4042-0_2CrossRefGoogle Scholar
Miller, C. and Speissegger, P., Expansions of the real line by open sets: o-minimality and open cores. Fund. Math. 162(1999), 193–208.Google Scholar
Miller, C. and Thamrongthanyalak, A., D-minimal expansions of the real field have the zero set property. Proc. Amer. Math. Soc. 146(2018), 5169–5179. https://doi.org/10.1090/proc/14144CrossRefGoogle Scholar
Nielsen, N., Die Gammafunktion. Band I. Handbuch der Theorie der Gammafunktion. Band II. Theorie des Integrallogarithmus und verwandter Transzendenten. Chelsea Publishing Co., New York, 1965.Google Scholar
Remmert, R., Classical topics in complex function theory. Graduate Texts in Mathematics, 172, Springer-Verlag, New York, 1998. https://doi.org/10.1007/978-1-4757-2956-6CrossRefGoogle Scholar
Sauzin, D., Introduction to 1-summability and resurgence. arxiv:1405.0356.Google Scholar
Speissegger, P., The Pfaffian closure of an o-minimal structure. J. Reine Angew. Math. 508(1999), 189–211. https://doi.org/10.1515/crll.1999.026Google Scholar
Titchmarsh, E. C., Introduction to the theory of Fourier integrals. Second ed., Oxford Univ. Press, London and New York, 1948.Google Scholar
Tychonievich, M. A., The set of restricted complex exponents for expansions of the reals. Notre Dame J. Form. Log. 53(2012), 175–186. https://doi.org/10.1215/00294527-1715671CrossRefGoogle Scholar
Tychonievich, M. A., Tameness results for expansions of the real field by groups. Ph.D. thesis, The Ohio State University, ProQuest LLC, Ann Arbor, MI, 2013.Google Scholar