Let 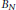${{B}_{N}}$ be the unit ball in 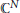${{\mathbb{C}}^{N}}$ and let 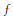$f$ be a function holomorphic and 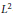${{L}^{2}}$-integrable in 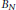${{B}_{N}}$. Denote by 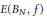$E\left( {{B}_{N}},\,f \right)$ the set of all slices of the form 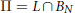$\Pi \,=\,L\,\cap \,{{B}_{N}}$, where 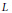$L$ is a complex one-dimensional subspace of 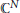${{\mathbb{C}}^{N}}$, for which 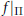$f{{|}_{\Pi }}$ is not 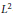${{L}^{2}}$-integrable (with respect to the Lebesgue measure on L). Call this set the exceptional set for 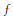$f$. We give a characterization of exceptional sets which are closed in the natural topology of slices.