Assume that 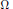$\Omega$ is a Hartogs domain in 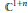${{\mathbb{C}}^{1+n}}$, defined as 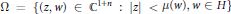$\Omega =\left\{ \left( z,w \right)\,\in \,{{\mathbb{C}}^{1+n}}\,:\left| z \right|\,<\,\mu \left( w \right),w\,\in H \right\}$, where 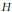$H$ is an open set in 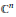${{\mathbb{C}}^{n}}$ and $\mu$ is a continuous function with positive values in 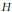$H$ such that –ln $\mu$ is a strongly plurisubharmonic function in 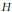$H$. Let 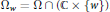${{\Omega }_{w}}=\Omega \cap \left( \mathbb{C}\times \left\{ w \right\} \right)$. For a given set $E$ contained in 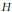$H$ of the type 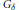${{G}_{\delta }}$ we construct a holomorphic function 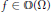$f\in \mathbb{O}\left( \Omega \right)$ such that

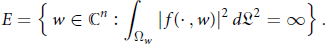$$E=\left\{ w\in {{\mathbb{C}}^{n}}:\int\limits_{{{\Omega }_{w}}}{{{\left| f\left( \cdot ,w \right) \right|}^{2}}d{{\mathfrak{L}}^{2}}=\infty } \right\}.$$