No CrossRef data available.
Published online by Cambridge University Press: 15 May 2023
In this paper, we construct explicit exponential bases of unions of segments of total measure one. Our construction applies to finite or infinite unions of segments, with some conditions on the gaps between them. We also construct exponential bases on finite or infinite unions of cubes in 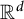 $\mathbb {R}^d$ and prove a stability result for unions of segments that generalize Kadec’s
$\mathbb {R}^d$ and prove a stability result for unions of segments that generalize Kadec’s 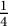 $\frac 14$-theorem.
$\frac 14$-theorem.
The research of this project started during the Summer 2022 REU program “AMRPU FIU” that took place at the Department of Mathematics and Statistics, Florida International University, which was supported by the NSA grant H982302210016 and the NSF (REU Site) grant DMS-2050971.