Published online by Cambridge University Press: 20 November 2018
We establish sufficient conditions on the shape of a set 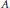 $A$ included in the space
$A$ included in the space 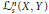 $\mathcal{L}_{s}^{n}\left( X,Y \right)$ of the
$\mathcal{L}_{s}^{n}\left( X,Y \right)$ of the  $n$-linear symmetric mappings between Banach spaces
$n$-linear symmetric mappings between Banach spaces 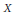 $X$ and
$X$ and  $Y$ , to ensure the existence of a
$Y$ , to ensure the existence of a 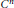 ${{C}^{n}}$-smooth mapping
${{C}^{n}}$-smooth mapping 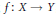 $f:X\to Y$, with bounded support, and such that
$f:X\to Y$, with bounded support, and such that 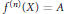 ${{f}^{\left( n \right)}}\left( X \right)=A$, provided that
${{f}^{\left( n \right)}}\left( X \right)=A$, provided that 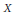 $X$ admits a
$X$ admits a 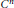 ${{C}^{n}}$-smooth bump with bounded
${{C}^{n}}$-smooth bump with bounded  $n$-th derivative and dens
$n$-th derivative and dens 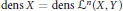 $\text{dens }X=\text{dens }{{\mathcal{L}}^{n}}\left( X,Y \right)$. For instance, when
$\text{dens }X=\text{dens }{{\mathcal{L}}^{n}}\left( X,Y \right)$. For instance, when 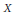 $X$ is infinite-dimensional, every bounded connected and open set
$X$ is infinite-dimensional, every bounded connected and open set 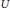 $U$ containing the origin is the range of the
$U$ containing the origin is the range of the  $n$-th derivative of such amapping. The same holds true for the closure of
$n$-th derivative of such amapping. The same holds true for the closure of 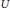 $U$, provided that every point in the boundary of
$U$, provided that every point in the boundary of 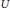 $U$ is the end point of a path within
$U$ is the end point of a path within 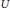 $U$. In the finite-dimensional case, more restrictive conditions are required. We also study the Fréchet smooth case for mappings from
$U$. In the finite-dimensional case, more restrictive conditions are required. We also study the Fréchet smooth case for mappings from 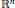 ${{\mathbb{R}}^{n}}$ to a separable infinite-dimensional Banach space and the Gâteaux smooth case for mappings defined on a separable infinite-dimensional Banach space and with values in a separable Banach space.
${{\mathbb{R}}^{n}}$ to a separable infinite-dimensional Banach space and the Gâteaux smooth case for mappings defined on a separable infinite-dimensional Banach space and with values in a separable Banach space.