Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T22:13:05.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact and Approximate Operator Parallelism

Published online by Cambridge University Press:  20 November 2018

Ali Zamani  and
Mohammad Sal Moslehian
Ali Zamani
Affiliation:
Department of PureMathematics, Center of Excellence in Analysis on Algebraic Structures (CEAAS), Ferdowsi University of Mashhad, Mashhad 91775, Iran. e-mail: [email protected], e-mail: [email protected] e-mail: [email protected]
Mohammad Sal Moslehian
Affiliation:
Department of PureMathematics, Center of Excellence in Analysis on Algebraic Structures (CEAAS), Ferdowsi University of Mashhad, Mashhad 91775, Iran. e-mail: [email protected], e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

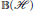Extending the notion of parallelism we introduce the concept of approximate parallelism in normed spaces and then substantially restrict ourselves to the setting of Hilbert space operators endowed with the operator norm. We present several characterizations of the exact and approximate operator parallelism in the algebra $\mathbb{B}\left( H \right)$ of bounded linear operators acting on a Hilbert space 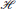$H$. Among other things, we investigate the relationship between the approximate parallelism and norm of inner derivations on 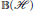$\mathbb{B}\left( H \right)$. We also characterize the parallel elements of a 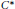${{C}^{*}}$-algebra by using states. Finally we utilize the linking algebra to give some equivalent assertions regarding parallel elements in a Hilbert 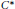${{C}^{*}}$-module.

Keywords

47A3046L0546L0847B4715A60C*-algebraapproximate parallelismoperator parallelismHilbert C*-module
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 207 - 224
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Arambašić, Lj. and Rajić, R., The Birkhoff–James orthogonality in Hilbert C*-modules. Linear Algebra Appl. 437 (2012), 1913–1929. http://dx.doi.org/10.1016/j.laa.2012.05.011 Google Scholar
[2] Arambašić, Lj. and Rajić, R., On some norm equalities in pre-Hilbert C*-modules. Linear Algebra Appl. 414 (2006), 19–28. http://dx.doi.org/10.1016/j.laa.2005.09.006 Google Scholar
[3] Bhatia, R. and Šemrl, P., Orthogonality of matrices and some distance problems. Linear Algebra Appl. 287 (1999), 77–85. http://dx.doi.org/10.1016/S0024-3795(98)10134-9 Google Scholar
[4] Chmielinśki, J., On an “-Birkhoff orthogonality. J. Inequal. Pure Appl. Math. 6 (2005), Art. 79, 7 pages (electronic).Google Scholar
[5] Dixmier, J., C*-Algebras. North-Holland, Amsterdam, 1981.Google Scholar
[6] Dragomir, S. S., On approximation of continuous linear functionals in normed linear spaces. An. Univ. Timis¸oara Ser. S¸ tiint¸. Mat. 29 (1991), 51–58. Google Scholar
[7] Fujii, J. I., Fujii, M., Moslehian, M. S., and Y. Seo, Cauchy–Schwarz inequality in semi-inner product C*-modules via polar decomposition. J. Math. Anal. Appl. 394 (2012), 835–840. http://dx.doi.org/10.1016/j.jmaa.2012.04.083 Google Scholar
[8] Fujii, M. and Nakamoto, R., An estimation of the transcendental radius of an operator. Math. Japon. 27 (1982), 637–638. Google Scholar
[9] Gustafson, K. E. and Rao, D. K. M., Numerical Range. The Field of Values of Linear Operators and Matrices. Universitext, Springer-Verlag, New York, 1997.Google Scholar
[10] Ilišević, D. and Turnšek, A., Approximately orthogonality preserving mappings on C*-modules. J.Math. Anal. Appl. 341 (2008), 298–308. http://dx.doi.org/10.1016/j.jmaa.2007.10.028 Google Scholar
[11] Lance, E. C., Hilbert C*-modules. A Toolkit for Operator Algebraists. London Math. Soc. Lecture Note Ser. 210, Cambridge University Press, Cambridge, 1995.Google Scholar
[12] Manuilov, V. M. and Troitsky, E. V., Hilbert C*-modules. In: Translations of Mathematical Monographs 226, Amer. Math. Soc., Providence, RI, 2005.Google Scholar
[13] McCarthy, C. A., cp. Israel J. Math. 5 (1967), 249–271. http://dx.doi.org/10.1007/BF02771613 Google Scholar
[14] Moslehian, M. S., An operator extension of the parallelogram law and related norm inequalities. Math. Inequal. Appl. 73 (2010), 3821–3831. Google Scholar
[15] Murphy, G. J., C*-Algebras and Operator Theory. Academic Press, New York, 1990.Google Scholar
[16] Raeburn, I. and Williams, D. P., Morita equivalence and continuous-trace C*-algebras. Math. Surveys Monogr. 60, American Mathematical Society, Providence, RI, 1998.Google Scholar
[17] Rieffel, M. A., Standard deviation is a strongly Leibniz seminorm. arxiv:1208.4072v2.Google Scholar
[18] Seddik, A., On the injective norm of ni =1Ai Bi and characterization of normaloid operators. Oper. Matrices 2 (2008), 67–77. http://dx.doi.org/10.7153/oam-02-04 Google Scholar
[19] Seddik, A., Rank one operators and norm of elementary operators. Linear Algebra Appl. 424 (2007), 177–183. http://dx.doi.org/10.1016/j.laa.2006.10.003 Google Scholar
[20] Werner, D., An elementary approach to the Daugavet equation. In: Interaction between functional analysis, harmonic analysis, and probability (Columbia, MO, 1994, Lecture Notes in Pure and Appl. Math. 175, Dekker, New York, 1996, 449–454. Google Scholar