Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T16:18:02.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of Eigenvalues along Rescaled Ricci Flow

Published online by Cambridge University Press:  20 November 2018

Junfang Li
Junfang Li*
Affiliation:
Department of Mathematics, University of Alabama at Birmingham, Birmingham, AL 35294 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

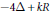In this paper, we discuss monotonicity formulae of various entropy functionals under various rescaled versions of Ricci flow. As an application, we prove that the lowest eigenvalue of a family of geometric operators $-4\Delta \,+\,kR$ is monotonic along the normalized Ricci flow for all 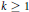$k\,\ge \,1$ provided the initial manifold has nonpositive total scalar curvature.

Keywords

58C4053C44monotonicity formulasRicci flow
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 127 - 135
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Akutagawa, K., Ishida, M., and LeBrun, C., Perelman's invariant, Ricci flow, and the Yamabe invariants of smooth manifolds. Arch. Math. 88 (2007), no. 1, 71–76.Google Scholar
[2] Cao, X., Eigenvalues of(-Δ R/2 ) on manifolds with nonnegative curvature operator. Math. Ann. 337 (2007), no. 2, 435–441.Google Scholar
[3] Cao, X., First eigenvalues of geometric operators under Ricci flow. arxiv:math.DG/0710.3947v1.Google Scholar
[4] Chow, B. and Knopf, D., The Ricci Flow: An Introduction. Mathematical Surveys and Monographs 110. American Mathematical Society, Providence, RI, 2004.Google Scholar
[5] Chow, B., S.-C. Chu, Glickenstein, D., et al., The Ricci Flow: Techniques and Applications. Part I. Geometric Aspects. Mathematical Surveys and Monographs 135. American Mathematical Society, Providence, RI, 2007.Google Scholar
[6] Hamilton, R. S., The formation of singularities in the Ricci flow. In: Surveys in Differential Geometry, Vol. II. Internat. Press, Cambridge, MA, 1995, pp. 7–136.Google Scholar
[7] Ivey, T., Ricci solitons on compact three-manifolds. Differential Geom. Appl. 3 (1993), no. 4, 301–307. http://dx.doi.org/10.1016/0926-2245(93)90008-O Google Scholar
[8] Li, J.-F., Eigenvalues and energy functionals with monotonicity formulae under Ricci flow. Math. Ann. 338 (2007), 927–946. http://dx.doi.org/10.1007/s00208-007-0098-y Google Scholar
[9] Oliynyka, T., Suneetab, V., and E.Woolgara, Irreversibility of world-sheet renormalization group flow. Phys. Lett. B,610 (2005), no. 1-2, 115–121. http://dx.doi.org/10.1016/j.physletb.2005.01.077 Google Scholar
[10] Perelman, G., The entropy formula for the Ricci flow and its geometric applications. arxiv:math.DG/0211159.Google Scholar