Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:32:26.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The Essential Spectrum of the Essentially Isometric Operator

Published online by Cambridge University Press:  20 November 2018

H. S. Mustafayev
H. S. Mustafayev*
Affiliation:
Yuzuncu Yıl University, Faculty of Science, Department of Mathematics, 65080, VAN-TURKEY e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $T$ be a contraction on a complex, separable, infinite dimensional Hilbert space and let 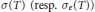$\sigma (T)\,(\text{resp}\text{.}\,{{\sigma }_{e}}(T))$ be its spectrum (resp. essential spectrum). We assume that $T$ is an essentially isometric operator; that is, 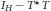${{I}_{H}}\,-\,T*T$ is compact. We show that if 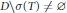$D\backslash \sigma (T)\,\ne \,\varnothing $, then for every 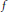$f$ from the disc-algebra

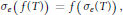$${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( {{\sigma }_{e}}\left( T \right) \right),$$

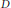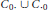where $D$ is the open unit disc. In addition, if $T$ lies in the class ${{C}_{0}}.\,\bigcup \,C{{.}_{0}}$, then

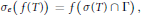$${{\sigma }_{e}}\left( f\left( T \right) \right)\,=\,f\left( \sigma \left( T \right)\,\bigcap \,\Gamma \right),$$

where $\Gamma $ is the unit circle. Some related problems are also discussed.

Keywords

47A1047A5347A6047B07Hilbert spacecontractionessentially isometric operator(essential) spectrumfunctional calculus
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 145 - 158
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Arveson, W., A short course on spectral theory. Graduate Texts in Mathematics, 209, Springer-Verlag, New York, 2002.Google Scholar
[2] Beauzamy, B., Introduction to operator theory and invariant subspaces. North-Holland Mathematical Library, 42, North Holland, Amsterdam, 1988.Google Scholar
[3] Conway, J. B., A course in functional analysis. Graduate Texts in Mathematics, 96, Springer-Verlag, New York, 1985.Google Scholar
[4] Gohberg, I. C. and Krein, M. G., Introduction to the theory of linear non-selfadjoint operators inHilbert space. (Russian), Nauka, Moscow, 1965.Google Scholar
[5] Kellay, K. and Zarrabi, M., Compact operators that commute with a contraction. Integral Equations Operator Theory 65 (2009), no. 4, 543–550. http://dx.doi.org/10.1007/s00020-009-1724-8 Google Scholar
[6] Larsen, R., Banach algebras. An introduction. Pure and Appled Mathematics, 24, Marcel Dekker Inc., New York, 1973.Google Scholar
[7] Muhly, P. S., Compact operators in the commutant of a contraction. J. Functional Analysis 8 (1971), 197–224. http://dx.doi.org/10.1016/0022-1236(71)90010-3 Google Scholar
[8] Mustafayev, H. S., Asymptotic behavior of polynomially bounded operators. C. R. Acad. Sci. Paris, Ser. I 348 (2010), no. 9–10, 517–520. http://dx.doi.org/10.1016/j.crma.2010.04.003 Google Scholar
[9] Nagy, B. Sz. and Foias, C., Harmonic analysis of operators on Hilbert space. (Russian), Mir, Moscow, 1970.Google Scholar
[10] Naĭmark, M. A., Normed rings. (Russian) second ed., Nauka, Moscow, 1968.Google Scholar
[11] Nikol'skiĭ, N. K., Lectures on the shift operator. (Russian), Nauka, Moscow, 1980.Google Scholar