Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T01:51:51.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalent Presentations of Modules Over Prüfer Domains

Published online by Cambridge University Press:  20 November 2018

Laszlo Fuchs  and
Sang Bum Lee
Laszlo Fuchs
Affiliation:
Department of Mathematics Tulane University New Orleans, Louisiana 70118 U.S.A., e-mail: [email protected]
Sang Bum Lee
Affiliation:
Department of Mathematical Education Sangmyung University Seoul 110-743 Korea
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 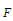$F$ and 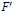${F}'$ are free 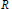$R$-modules, then 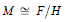$M\cong F/H$ and 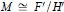$M\,\cong \,{F}'\,/\,{H}'$ are viewed as equivalent presentations of the 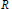$R$-module 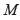$M$ if there is an isomorphism 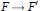$F\,\to \,{F}'$ which carries the submodule 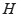$H$ onto 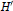${H}'$. We study when presentations of modules of projective dimension 1 over Prüfer domains of finite character are necessarily equivalent.

Keywords

13C11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 151 - 157
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Brewer, J. and Klingler, L., Pole assignability and the invariant factor theorem in Prüfer domains and Dedekind domains. J.Algebra 114 (1987), 536–545.Google Scholar
2. Cohen, J. and Gluck, H., Stacked bases for modules over principal ideal domains. J. Algebra 14 (1970), 493–505.Google Scholar
3. Erdőos, J., Torsion-free factor groups of free abelian groups and a classification of torsion-free abelian groups. Publ. Math. Debrecen 5 (1957), 172–184.Google Scholar
4. Fuchs, L., Abelian Groups. Akadémiai Kiadó, Budapest, 1958.Google Scholar
5. Fuchs, L., Note on modules of projective dimension one. In: Abelian Group Theory, Gordon and Breach Science Publishers, New York etc., 1986.Google Scholar
6. Heitmann, R. C. and Levy, L. S., 1 1/2 and 2 generator ideals in Prüfer domains. RockyMountain J. Math. 5 (1975), 361–373.Google Scholar
7. Hill, P. and Megibben, C., Generalizations of the stacked bases theorem. Trans.Amer.Math. Soc. 312 (1989), 377–402.Google Scholar
8. Kaplansky, I., Modules over Dedekind rings and valuation rings. Trans. Amer.Math. Soc. 72(1952), 327–340.Google Scholar
9. Levy, L. S., Invariant factor theorem for Prüfer domains of finite character. J. Algebra 106 (1987), 259–264.Google Scholar