Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T13:11:55.653Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence of Lp Stability and Exponential Stability of Nonlinear Lipschitzian Semigroups

Published online by Cambridge University Press:  20 November 2018

Song Xueli  and
Peng Jigen
Song Xueli
Affiliation:
Department of Mathematics and Information Science, Chang’an University, Xi’an 710064, ChinaandDepartment of Mathematics, Xi’an Jiaotong University, Xi’an 710049, Chinae-mail: [email protected]
Peng Jigen
Affiliation:
Department of Mathematics, Xi’an Jiaotong University, Xi’an 710049, Chinae-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

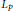${{L}_{p}}$ stability and exponential stability are two important concepts for nonlinear dynamic systems. In this paper, we prove that a nonlinear exponentially bounded Lipschitzian semigroup is exponentially stable if and only if the semigroup is 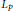${{L}_{p}}$ stable for some 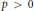$p\,>\,0$. Based on the equivalence, we derive two sufficient conditions for exponential stability of the nonlinear semigroup. The results obtained extend and improve some existing ones.

Keywords

34D0547H20exponentially stableLp stablenonlinear Lipschitzian semigroups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 882 - 889
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Arendt, W., Batty, C. J. K., Hieber, M., and Neubrander, F., Vector-Valued Laplace Transforms and Cauchy Probems. Monographs in Mathematics 96. Birkhäuser Verlag, Basel, 2001.Google Scholar
[2] Barbu, V., Nonlinear Semigroups and Differential Equations in Banach Spaces. Noordhoff, Leiden, 1976.Google Scholar
[3] Belleni-Morante, A. and Mcbride, A. C., Applied Nonlinear Semigroups: An Introduction. JohnWiley & Sons, Chichester, 1998.Google Scholar
[4] Datko, R., Extending a theorem of A. M. Liapunov to Hilbert space. J. Math. Anal. Appl. 32(1970), 610–616. http://dx.doi.org/10.1016/0022-247X(70)90283-0 Google Scholar
[5] Engel, K. J. and Nagel, R., One-parameter Semigroups of Linear Evolution Equations. Graduate Texts in Mathematics 194. Springer-Verlag, New York, 2000.Google Scholar
[6] Fattorini, H. O., The Cauchy Prolem. Encyclopedia of Mathematics and its Applications18. Addison-Wesley, Reading, MA, 1983.Google Scholar
[7] Goldsein, J. A., Semigroups of Linear Operators and Applications. Oxford Mathematical Monographs, Oxford University Press, New York, 1985.Google Scholar
[8] Hahn, W., Stability of Motion. Die Grundlehren der mathematischen Wissenschaften 138. Springer-Verlag, New York, 1967.Google Scholar
[9] Ichikawa, A., Stability and optimal control of stochastic evolution equations. In: Distributed Parameter Control Systems: Theory and Application, Chapter 5, Pergamon Press, New York, 1982.Google Scholar
[10] Ichikawa, A., Equivalence of Lp stability and exponential stability for a class of nonlinear semigroups. Nonlinear Anal. 8(1984), no. 7, 805–815. http://dx.doi.org/10.1016/0362-546X(84)90078-6 Google Scholar
[11] Kobayshi, Y. and Tanaka, N., Semigroups of Lipschitz operators. Adv. Differential Equations 6(2001), no. 5, 613–640.Google Scholar
[12] Kobayshi, Y. and Tanaka, N., Convergence and approximation of semigroups of Lipschitz operators. Nonlinear Anal. 61(2005), no. 5, 781–821. http://dx.doi.org/10.1016/j.na.2005.01.040 Google Scholar
[13] Miyadera, I., Nonlinear Semigroups. Translations of Mathematical Monographs 109. American Mathematical Society, Providence, RI, 1992.Google Scholar
[14] van Neerven, J. M. A. A., The Asymptotic Behviour of Semigroups of Linear Operators. Operator Theory: Advances and Applications 88. Birkhäuser Verlag, Basel, 1996.Google Scholar
[15] Pazy, A., On the applicability of Lyapunov's theorem in Hilbert space. SIAM J. Math. Anal. 3(1972), 291–294. http://dx.doi.org/10.1137/0503028 Google Scholar
[16] Pazy, A., Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Mathematical Sciences 44. Springer-Verlag, New York, 1983.Google Scholar
[17] Peng, J. G., Theoretical Researchs on Nonlinear Lipschitz Opertors and their Applications. (in Chinese), Ph.D. dissertation, Xi’an Jiaotong University, 1998.Google Scholar
[18] Peng, J. G. and Xu, Z. B., On asymptotic behaviours of nonlinear semigroup of Lipschitz operators with applications.(in Chinese), Acta Math. Sinica 45(2002), no. 6, 1099–1106.Google Scholar
[19] Peng, J. G. and Xu, Z. B., A novel dual approach to nonlinear semigroups of Lipschitz operators. Trans. Amer. Math. Soc. 357(2005), no. 1, 409–424. http://dx.doi.org/10.1090/S0002-9947-04-03635-9 Google Scholar
[20] Zabczyk, J., Remarks on the control of discrete-time distributed parameter systems. SIAM J. Control 12(1974), 721–735. http://dx.doi.org/10.1137/0312056 Google Scholar