A well-known theorem of Schütte (1963) gives a sharp lower bound for the ratio of the maximum and minimum distances between 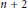$n\,+\,2$ points in $n$-dimensional Euclidean space. In this note we adapt Bárány’s elegant proof (1994) of this theorem to the space 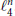$\ell _{4}^{n}$. This gives a new proof that the largest cardinality of an equilateral set in 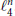$\ell _{4}^{n}$ is 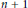$n\,+\,1$ and gives a constructive bound for an interval $\left( 4\,-\,{{\varepsilon }_{n}},\,4\,+\,{{\varepsilon }_{n}} \right)$ of values of 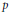$p$ close to 4 for which it is known that the largest cardinality of an equilateral set in 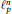$\ell _{p}^{n}$ is 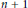$n\,+\,1$.