No CrossRef data available.
Article contents
Equalizing the Coefficients in a Product of Polynomials
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In 1959, Moser [4] posed the following problem: how should a pair of n-sided dice be loaded (identically) so that, on throwing the dice, the frequency of the most frequently occurring sum is as small as possible? This can be recast in the following form: determine for each n(≥1), the polynomial Pn(x) which minimizes the maximum coefficient in the polynomial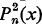 
subject to the conditions that the coefficients of Pn(x) are nonnegative and sum to unity.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1973
References
1.
Barrodale, I. and Roberts, F. D. K., Application of mathematical programming to lp approximation, in nonlinear programming, Rosen, Mangasarian and Ritter, eds., Academic Press, New York, (1970), 447–464.Google Scholar
2.
Clements, G. F., On a min-max problem of Leo Moser, J. Combinatorial Theory, 4 (1968), 36–39.Google Scholar
3.
Fröberg, C E., Introduction to numerical analysis, Addison-Wesley, Reading, Mass., 1969.Google Scholar
4.
Moser, L., in Report of the Institute in the Theory of Numbers, University of Colorado, June 21-July 17 (1959), p. 342.Google Scholar
5.
Moser, L., On the representation of 1, 2,…, n by sums, Acta Arith. VI (1960), 11–13.Google Scholar
You have
Access