Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T12:46:16.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary Remarks on Multiply Monotonic Functions and Sequences(1)

Published online by Cambridge University Press:  20 November 2018

M. E. Muldoon
M. E. Muldoon*
Affiliation:
York University, Downsview, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A function f(x) is said to be completely monotonic on (0, ∞) if

1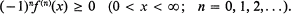

Familiar examples of such functions are given by f(x) = exp(—αx) and f(x) = (x+β)-α, where α ≥ 0, β ≥ 0. A discussion of completely monotonic functions is given in [5, Ch. IV].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 1 , January 1971 , pp. 69 - 72
Copyright
Copyright © Canadian Mathematical Society 1971

Footnotes

(1)

This is a revised version of a note written while the author attended the Summer Research Institute of the Canadian Mathematical Congress, Université de Montréal, 1969. The writer is indebted to Professor Lee Lorch for some helpful comments.

References

1. Dubourdieu, J., Sur un théorème de M. S. Bernstein relatif á la transformation de Laplace- Stieltjes, Compositio Math. 7 (1939-1940), 96-111.Google Scholar
2. Lorch, Lee and Moser, Leo, A remark on completely monotonie sequences with an application to summability, Canad. Math. Bull. 6 (1963), 171-173.Google Scholar
3. Lorch, Lee and Szego, Peter, Higher monotonicity properties of certain Sturm-Liouville functions, Acta Math. 109 (1963), 55-73.Google Scholar
4. Schoenberg, I. J., On integral representations of completely monotone and related functions (abstract), Bull. Amer. Math. Soc. 47 (1941), p. 208.Google Scholar
5. Widder, D. V., The Laplace transform, Princeton Univ. Press, Princeton, N.J., 1941.Google Scholar
6. Williamson, R. E., Multiply monotone functions and their Laplace transforms, Duke Math. J. 23 (1956), 189-207.Google Scholar