Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T04:14:41.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary Proofs of the Extremal Properties of the Eigenvalues of the Sturm-Liouville Equation

Published online by Cambridge University Press:  20 November 2018

Paul R. Beesack
Paul R. Beesack*
Affiliation:
McMaster University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If the Sturm-Liouville eigenvalue problem

1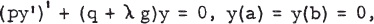

is first approached from the standpoint of differential equations theory - as opposed, say, to the calculus of variations, or the theory of integral equations - the extremal properties of the eigenvalues seem to be generally regarded as lying beyond the scope of the theory. Thus, neither in the standard work of Bocher [l], nor in the recent work of Coddington and Levinson [2] is any mention made of this topic. Collatz [3, 166-8] gives an elementary proof of the minimum property of the least positive eigenvalue of (1.1), and a brief indication of how this argument can be extended to the higher eigenvalues. The purpose of this paper is to consolidate this elementary approach, and to extend it to cover the singular cases where either the interval is infinite, or one or more of the coefficients are singular at the end-points.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 3 , Issue 1 , 01 January 1960 , pp. 59 - 77
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Bocher, M., Le?ons sur les m?thodes de Sturm, (Paris, 1917).Google Scholar
2. Coddington, E. and Levinson, N., Theory of Ordinary Differ ential Equations, (New York, 1955).Google Scholar
3. Collatz, L., Eigenwertprobleme und ihre numerische Behandlung, (New York, 1948).Google Scholar
4. Courant, R., and Hilbert, D., Methods of Mathematical Physics, vol. 1, (New York, 1953).Google Scholar