Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T16:27:45.144Z Has data issue: false hasContentIssue false
  • English
  • Français

D-Spaces and Resolution

Published online by Cambridge University Press:  20 November 2018

Zineddine Boudhraa
Zineddine Boudhraa*
Affiliation:
Bowie State University, Department of Mathematics, Bowie, Maryland 20715, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A space X is a D-space if, for every neighborhood assignment f there is a closed discrete set D such that 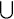f(D) = X. In this paper we give some necessary conditions and some sufficient conditions for a resolution of a topological space to be a D-space. In particular, if a space X is resolved at each x ∊ X into a D-space Yx by continuous mappings fx: X − {x} → Yx, then the resolution is a D-space if and only if 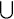{x} × Bd(Yx) is a D-space.

Keywords

Primary: 54D2054B99secondary: 54D1054D30D-spaceneighborhood assignmentresolutionboundary
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 40 , Issue 4 , 01 December 1997 , pp. 395 - 401
Copyright
Copyright © Canadian Mathematical Society 1997

References

1. van Douwen, E. K. and Pfeffer, W. F., Some Properties of the Sorgenfrey Line and Related Spaces. Pacific J. Math. (2) 81 (1979).Google Scholar
2. Engelking, R., General Topology. Polish Scientific Publishers, 1977.Google Scholar
3. Watson, S., The Construction of Topological Spaces. Recent Progress in General Topology, North-Holland, 1992.Google Scholar