No CrossRef data available.
Article contents
Domains of Injective Holomorphy
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A domain 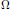 $\Omega $ is called a domain of injective holomorphy if there exists an injective holomorphic function
$\Omega $ is called a domain of injective holomorphy if there exists an injective holomorphic function 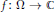 $f\,:\,\Omega \,\to \,\mathbb{C}$ that is non-extendable. We give examples of domains that are domains of injective holomorphy and others that are not. In particular, every regular domain
$f\,:\,\Omega \,\to \,\mathbb{C}$ that is non-extendable. We give examples of domains that are domains of injective holomorphy and others that are not. In particular, every regular domain 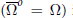 $(\overset{\multimap }{\mathop{\Omega }}\,\,=\,\Omega )$ is a domain of injective holomorphy, and every simply connected domain is a domain of injective holomorphy as well.
$(\overset{\multimap }{\mathop{\Omega }}\,\,=\,\Omega )$ is a domain of injective holomorphy, and every simply connected domain is a domain of injective holomorphy as well.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1] Dienes, P., The Taylor series: an introduction to the theory of functions of a complex variable.
Dover Publications, Inc., New York, 1957.Google Scholar
[2] Fuks, B. A., Special chapters in the theory of analytic functions of several complex variables. Translated from the Russian by Jeffrey, A. and Mugibayashi, N.. Translations of Mathematical Monographs, 14, American Mathematical Society, Providence, RI, 1965.Google Scholar
[3] Gauthier, P. M., The Cauchy theorem for domains of arbitrary connectivity on Riemann surfaces. In: Geometric function theory in several complex variables, World Sci. Publ., River Edge, NJ, 2004, pp. 123–142.Google Scholar
[4] Kahane, J.-P., Baire's category theorem and trigonometric series. J. Anal. Math.
80(2000), 143–182. http://dx.doi.org/10.1007/BF02791536
Google Scholar
[5] Nestoridis, V., Non extendable holomorphic functions. Math. Proc. Cambridge Philos. Soc.
139(2005), no. 2, 351–360. http://dx.doi.org/10.1017/S0305004105008728
Google Scholar
[7] Saks, S. and Zygmund, A., Analytic functions.
Second ed., Monografie Matematyczne, 28, Państwowe Wydawnietwo Naukowe, Warsaw, 1965.Google Scholar


