No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let X be a projective nonsingular variety over a real closed field R such that the set X(R) of R-rational points of X is nonempty. Let ClR(X) = Cl(X)/Γ(X), where Cl(X) is the group of classes of linearly equivalent divisors on X and Γ(X) is the subgroup of Cl(X) consisting of the classes of divisors whose restriction to some neighborhood of X(R) in X is linearly equivalent to 0. It is proved that the group ClR(X) is isomorphic to (Z/2)s for some non-negative integer s. Moreover, an upper bound on s is given in terms of the Z/2-dimension of the group cohomology modules of Gal(C/R), where 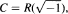 , with values in the Néron-Severi group and the Picard variety of Xc = X xR C.
, with values in the Néron-Severi group and the Picard variety of Xc = X xR C.