Hostname: page-component-7bb8b95d7b-l4ctd Total loading time: 0 Render date: 2024-09-20T23:11:13.607Z Has data issue: false hasContentIssue false
  • English
  • Français

A Divisor Problem for Values of Polynomials

Published online by Cambridge University Press:  20 November 2018

Armel Mercier  and
Werner Georg Nowak
Armel Mercier
Affiliation:
Département de mathématiques Université du Québec à Chicoutimi 555 boul. Université Chicoutimi, Prov. de Québec G7H2B1, Canada
Werner Georg Nowak
Affiliation:
Institut für Mathematik der Universitât fur Bodenkultur Greg or Mendel-Strafie 33 A-1180 Wien, Austria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article we investigate the average order of the arithmetical function

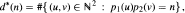
where p1(t), p2(t) are polynomials in Z [t], of equal degree, positive and increasing for t ≥ 1. Using the modern method for the estimation of exponential sums ("Discrete Hardy-Littlewood Method"), we establish an asymptotic result which is as sharp as the best one known for the classical divisor problem.

Résumé

Résumé

Dans cet article, on étudie l'ordre moyen de la fonction arithmétique

où p1(t),p2(t) sont des polynômes dans Z[t], de degrés égaux, qui sont positifs et croissants pour t ≥ 1. En utilisant la méthode moderne pour l'estimation de sommes exponentielles ("méthode discrète de Hardy-Littlewood"), on obtient un comportement asymptotique, aussi précis que le meilleur résultat connu, concernant le problème classique des diviseurs.

Keywords

10H2510G1010J25.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 1 , 01 March 1992 , pp. 108 - 115
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Flicker, F., Einfuhrung in die Gitterpunktlehre, Birkhàuser, Basel-Boston-Stuttgart, 1982.Google Scholar
2. Huxley, M.N., Exponential sums and lattice points, Proc. London Math. Soc. (3) 60 (1990), 471–502.Google Scholar
3. Iwaniec, H., and Mozzochi, C.J., On the divisor and circle problems, J. Number Th. 29 (1988), 60–93.Google Scholar
4. Krâtzel, E., Lattice points, Kluwer Acad. Publ., Dordrecht-Boston-London, 1988.Google Scholar
5. Kuba, G., Neuere Methoden der Gitterpunktlehre und spezielle zahlentheoretische Funktionen, Thesis, Vienna University, 1990.Google Scholar
6. Kuba, G., and Nowak, W.G., On representations of positive integers as a sum of two polynomials, Arch. Math. (Basel), to appear.Google Scholar
7. Miiller, W., and Nowak, W.G., Lattice points in planar domains: Applications of Huxley's “Discrete Hardy- Littlewood method”, in: “Number theoretic analysis”, Vienna 1988-89, Springer Lecture Notes 1452 (eds. E. Hlawka and R. F. Tichy), 1990, pp. 139–164.Google Scholar
8. Nowak, W.G., On a result of Smith and Subbarao concerning a divisor problem, Can. Math. Bull. 27 (1984), 501–504.Google Scholar
9. Nowak, W.G., On a divisor problem in arithmetic progressions. J. Number Theory 31 (1989), 174–182.Google Scholar
10. Smith, R.A., and Subbarao, M.V., The average number of divisors in an arithmetic progression, Can. Math. Bull. 24 (1981), 37–41.Google Scholar
11. Varbanec, P.D., and Zarzycki, P., Divisors of integers in arithmetic progressions, Can. Math. Bull. 33 ( 1990), 129–134.Google Scholar