The integers coprime to $n$ are called the totatives of $n$. D. H. Lehmer and Paul Erdős were interested in understanding when the number of totatives between 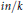$in/k$ and 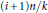$\left( i\,+1 \right)n/k$ are 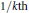$1/k\text{th}$ of the total number of totatives up to $n$. They provided criteria in various cases. Here we give an “if and only if” criterion which allows us to recover most of the previous results in this literature and to go beyond, as well to reformulate the problem in terms of combinatorial group theory. Our criterion is that the above holds if and only if for every odd character $\chi \,\left( \bmod \,\kappa \right)\,\left( \text{where}\,\kappa :=k/\gcd \left( k,\,n/{{\Pi }_{p|n}}p \right) \right)$ there exists a prime 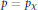$p={{p}_{\chi }}$ dividing $n$ for which 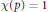$\chi \left( p \right)=1.$