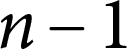Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T23:40:12.117Z Has data issue: false hasContentIssue false
  • English
  • Français

The Distance from a Rank $n-1$ Projection to the Nilpotent Operators on 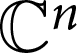$\mathbb {C}^n$

Part of: General theory of linear operators Basic linear algebra

Published online by Cambridge University Press:  02 April 2020

Zachary Cramer
Zachary Cramer*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, OntarioN2L 3G1
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Building on MacDonald’s formula for the distance from a rank-one projection to the set of nilpotents in 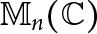$\mathbb {M}_n(\mathbb {C})$, we prove that the distance from a rank 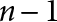$n-1$ projection to the set of nilpotents in 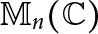$\mathbb {M}_n(\mathbb {C})$ is 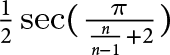$\frac {1}{2}\sec (\frac {\pi }{\frac {n}{n-1}+2} )$. For each 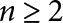$n\geq 2$, we construct examples of pairs 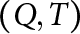$(Q,T)$ where Q is a projection of rank 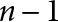$n-1$ and 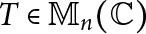$T\in \mathbb {M}_n(\mathbb {C})$ is a nilpotent of minimal distance to Q. Furthermore, we prove that any two such pairs are unitarily equivalent. We end by discussing possible extensions of these results in the case of projections of intermediate ranks.

Keywords

projectionnilpotentmatrixoperator

MSC classification

Primary: 47A58: Operator approximation theory
Secondary: 15A99: Miscellaneous topics
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 54 - 74
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by NSERC (Canada).

References

Arveson, W. B., Interpolation problems in nest algebras. J. Functional Analysis 20(1975), 208–233. https://doi.org/10.1016/0022-1236(75)90041-5CrossRefGoogle Scholar
Bini, D., Eidelman, Y., Gemignani, L., and Gohberg, I., The unitary completion and QR iterations for a class of structured matrices. Math. Comp. 77(2008), 353–378. https://doi.org/10.1090/S0025-5718-07-02004-2CrossRefGoogle Scholar
Hedlund, J. H., Limits of nilpotent and quasinilpotent operators. Michigan Math. J. 19(1972), 249–255.Google Scholar
Herrero, D. A., Normal limits of nilpotent operators. Indiana Univ. Math. J. 23(1974), 1097–1108.CrossRefGoogle Scholar
Herrero, D. A., Unitary orbits of power partial isometries and approximation by block-diagonal nilpotents. In: Topics in modern operator theory. Springer, 1981, pp. 171–210.CrossRefGoogle Scholar
MacDonald, G. W., Distance from projections to nilpotents. Canad. J. Math. 47(1995), 841–851. https://doi.org/10.4153/CJM-1995-043-3CrossRefGoogle Scholar
MacDonald, G. W., Distance from idempotents to nilpotents. Canad. J. Math. 59(2007), 638–657. https://doi.org/10.4153/CJM-2007-027-xCrossRefGoogle Scholar
Power, S. C., The distance to upper triangular operators. Math. Proc. Cambridge Philos. Soc. 88(1980), 327–329. https://doi.org/10.1017/S030500410057637CrossRefGoogle Scholar
Salinas, N., On the distance to the set of compact perturbations of nilpotent operators. J. Operator Theory 3(1980), 179–194.Google Scholar