Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T08:54:39.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Disk Packings which have Non-Extreme Exponents

Published online by Cambridge University Press:  20 November 2018

David W. Boyd
David W. Boyd*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let U be an open set in the Euclidean plane which has finite area. A complete (or solid) packing of U is a sequence of pairwise disjoint open disks C={Dn}, each contained in U and whose total area equals that of U. A simple osculatory packing of U is one in which the disk Dn has, for each n, the largest radius of disks contained in 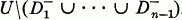(S- denotes the closure of the set U.) If rn is the radius of Dn, then the exponent of the packing, e(C, U) is the infimum of real numbers t for which 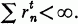In the sequel we refer to a complete packing simply as a packing.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 3 , September 1972 , pp. 341 - 344
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Boyd, D. W., Lower bounds for the disk packing constant, Math. Comp. 24 (1970), 697-704.Google Scholar
2. Boyd, D. W., The disk packing constant, Aequationes Mathematicae, (to appear).Google Scholar
3. Melzak, Z. A., Infinite packings of disks, Canad. J. Math. 18 (1966), 838-852.Google Scholar
4. Melzak, Z. A., On the solid-packing constant for circles, Math. Comp. 23 (1969), 169-172.Google Scholar
5. Wilker, J. B., Open disk packings of a disk, Canad. Math. Bull. 10 (1967), 395-415.Google Scholar