Published online by Cambridge University Press: 04 October 2019
Let 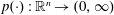 $p(\cdot ):\mathbb{R}^{n}\rightarrow (0,\infty )$ be a variable exponent function satisfying the globally log-Hölder continuous condition. In this paper, we obtain the boundedness of paraproduct operators
$p(\cdot ):\mathbb{R}^{n}\rightarrow (0,\infty )$ be a variable exponent function satisfying the globally log-Hölder continuous condition. In this paper, we obtain the boundedness of paraproduct operators 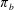 $\unicode[STIX]{x1D70B}_{b}$ on variable Hardy spaces
$\unicode[STIX]{x1D70B}_{b}$ on variable Hardy spaces 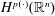 $H^{p(\cdot )}(\mathbb{R}^{n})$, where
$H^{p(\cdot )}(\mathbb{R}^{n})$, where 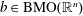 $b\in \text{BMO}(\mathbb{R}^{n})$. As an application, we show that non-convolution type Calderón–Zygmund operators
$b\in \text{BMO}(\mathbb{R}^{n})$. As an application, we show that non-convolution type Calderón–Zygmund operators 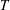 $T$ are bounded on
$T$ are bounded on  $H^{p(\cdot )}(\mathbb{R}^{n})$ if and only if
$H^{p(\cdot )}(\mathbb{R}^{n})$ if and only if 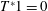 $T^{\ast }1=0$, where
$T^{\ast }1=0$, where 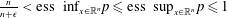 $\frac{n}{n+\unicode[STIX]{x1D716}}<\text{ess inf}_{x\in \mathbb{R}^{n}}p\leqslant \text{ess sup}_{x\in \mathbb{R}^{n}}p\leqslant 1$ and
$\frac{n}{n+\unicode[STIX]{x1D716}}<\text{ess inf}_{x\in \mathbb{R}^{n}}p\leqslant \text{ess sup}_{x\in \mathbb{R}^{n}}p\leqslant 1$ and  $\unicode[STIX]{x1D716}$ is the regular exponent of kernel of
$\unicode[STIX]{x1D716}$ is the regular exponent of kernel of  $T$. Our approach relies on the discrete version of Calderón’s reproducing formula, discrete Littlewood–Paley–Stein theory, almost orthogonal estimates, and variable exponents analysis techniques. These results still hold for variable Hardy space on spaces of homogeneous type by using our methods.
$T$. Our approach relies on the discrete version of Calderón’s reproducing formula, discrete Littlewood–Paley–Stein theory, almost orthogonal estimates, and variable exponents analysis techniques. These results still hold for variable Hardy space on spaces of homogeneous type by using our methods.
The project was sponsored by the Natural Science Foundation of Jiangsu Province of China (grant no. BK20180734), National Natural Science Foundation of China (No.11901309), the Natural Science Research of Jiangsu Higher Education Institutions of China (grant no. 18KJB110022), and Nanjing University of Posts and Telecommunications Science Foundation (grant nos. NY219114, NY217151).